
Читайте также:
|
16.1.3.5.1. Если функция 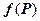 интегрируема по области
интегрируема по области 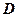 , и для
, и для  выполняется
выполняется  , то
, то 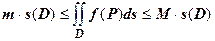 .
.
Док-во. 






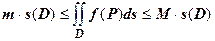 (цифрами над знаками импликации обозначены номера применяемых ранее доказанных свойств).
(цифрами над знаками импликации обозначены номера применяемых ранее доказанных свойств).
16.1.3.5.2. Если функция 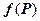 интегрируема по области
интегрируема по области 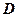 , то
, то  .
.
Док-во. Эти неравенства непосредственно следуют из того, что  и свойства 16.1.3.4. Интегрирование неравенств.
и свойства 16.1.3.4. Интегрирование неравенств.
16.1.3.6. Теорема о среднем. Если функция 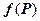 непрерывна на области
непрерывна на области 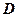 , то существует точка
, то существует точка  , такая что
, такая что 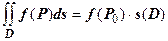 .
.
Док-во. Непрерывная на ограниченной замкнутой области 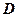 функция
функция 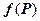 принимает в некоторых точках этой области своё минимальное
принимает в некоторых точках этой области своё минимальное  и максимальное
и максимальное  значения. Так как
значения. Так как  , то
, то 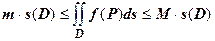 , или
, или  . Непрерывная функция принимает, кроме того, любое значение, заключённое между
. Непрерывная функция принимает, кроме того, любое значение, заключённое между  и
и  , в частности, значение
, в частности, значение 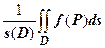 . Следовательно,
. Следовательно,  , откуда и следует доказываемое утверждение.
, откуда и следует доказываемое утверждение.
Дата добавления: 2015-07-20; просмотров: 101 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства двойного интеграла. | | | Вычисление двойного интеграла. Двукратный (повторный) интеграл. |