Читайте также:
|
16.1.3.1. Линейность. Если функции 
, 
интегрируемы по области 
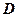, то их линейная комбинация 
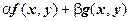тоже интегрируема по област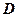и , и 
.
Док-во. Для интегральных сумм справедливо равенство 
. Переходя к пределу при 
и пользуясь свойствами пределов, рассмотренными в разделе 4.4.6. Арифметические действия с пределами (конкретно, свойствами 4.4.10.1 и 4.4.10.2), получим требуемое равенство.
16.1.3.2. 
Аддитивность. Если область 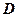является объединением двух областей 
и 
, не имеющих общих внутренних точек, то 
.
Док-во. Пусть область разбита на подобласти 
, область разбита на подобласти 
. Тогда объединение этих разбиений даст разбиение области :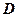 
на 
подобластей. Интегральная сумма по области 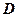равна сумме сумм по областям и : 
. Как и в предыдущем случае, переходя к пределу при 
, получим требуемое равенство.
16.1.3.3.Интеграл от единичной функции по области 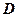равен площади этой области: 
.
Док-во: Для любого разбиения 
, т.е. не зависит ни от разбиения, ни от выбора точек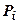 
. Предел постоянной равен этой постоянной, поэтому 
.
16.1.3.4. Интегрирование неравенств. Если в любой точке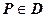 
выполняется неравенство 
, и функции 
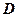интегрируемы по области , то 
.
Док-во. В любой точке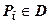 
выполняется неравенство 
, поэтому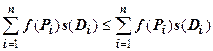 
. По теореме о переходе к пределу в неравенствах отсюда следует требуемое утверждение.
Дата добавления: 2015-07-20; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Двойной интеграл. | | | Теоремы об оценке интеграла. |