Симметрия волновой функции

Электронная оболочка молекулы является фермионной системой и ее волновая функция должна удовлетворять принципу Паули: если два любые электрона обмениваются состояниями (АСО), то глобальная волновая функция умножается на число –1 (перестановочная антисимметрия). Если антисимметричная функция построена в виде линейной комбинации, то все ее слагаемые должны либо сами по себе быть антисимметричны, либо образовывать друг с другом антисимметричные комбинации. Это требование накладывает существенные ограничения на значения коэффициентов С_i.

Исследуем перестановочную симметрию базисных функций. Для этого надо просто поменять местами первый и второй сомножители и посмотреть, что получится. Например, при действии оператора перестановки Р ₁₂ на функцию Ф₁ получится не эта же самая функция, умноженная на какое либо число, а совсем другая функция, а именно — Ф₃:

Р ₁₂ [ Ф₁ ]= Р ₁₂ [(Аa × Вb)] = Вb × Аa = Ф₃ (¹ k × Ф₁)

Следовательно, функция Ф₁ не является собственной для оператора перестановки и не обладает требуемой антисимметричностью. Аналогичный вывод получим для функции Ф₃: она переходит не сама в себя, а в функцию Ф₁. Для преодоления указанной трудности можно воспользоваться специальным математическим приемом — "симметризацией". Всякий раз, когда имеются несимметричные объекты, переходящие не сами в себя, а друг в друга, из них можно построить линейную комбинацию, обладающую симметрией. Например, построим разность:

Ф₁₃ = Ф₁ – Ф₃ = Аa × Вb – Вb × Аa

Такая комбинация уже является антисимметричной:

Р ₁₂ [ Ф₁₃ ] = Р ₁₂ [(Аa × Вb – Вb × Аa) = (Вb × Аa – Аa × Вb) =

= (–1) × (Аa × Вb – Вb × Аa) = (–1) × Ф₁₃

Отсюда следует вывод: коэффициенты при первой и третьей базисных функциях должны быть одинаковы по величине и противоположны по знаку: С ₁ = – С ₃. Проделав аналогичный анализ для остальных базисных функций, можно обнаружить еще три антисимметричные комбинации:

Ф₂₄ = Ф₂ – Ф₄ = Аb × Вa – Вa × Аb (С ₂ = – С ₄)

Ф₅₇ = Ф₅ – Ф₇ = Аa × Вa – Вa × Аa (С ₅ = – С ₇)

Ф₆₈ = Ф₆ – Ф₈ = Аb × Вb – Вb × Аb (С ₆ = – С ₈)

Функции ионных РФ, построенные в виде определителя, уже сами по себе являются антисимметричными. В результате, из десяти неизвестных коэффициентов остается только шесть.

Кроме перестановок электронов всякая молекула характеризуется расположением атомных ядер в пространстве, которое можно описать точечной группой симметрии. Очевидно, что электронная оболочка молекул также должна быть симметричной, поскольку поведение электронов определяется влиянием ядер. Плотность электронного облака определяется квадратом волновой функции. Ясно, что в пространственно симметричных (относительно ядерного остова) точках эти квадраты должны быть равны между собой, а значения самой волновой функции в симметричных точках могут отличаться только знаком. Таким образом, при действии любого из операторов пространственной симметрии F на волновую функцию она должна переходить сама в себя; при этом волновая функция может вся целиком умножаться на число +1 или –1. Следовательно, для молекулы водорода возможно всего два типа электронных состояний:

пространственно симметричные F [ Фs ] = (+1) × Фs

пространственно антисимметричные F [ Фas ] = (–1) × Фas

Для молекулы Н₂ в качестве операции симметрии чаще всего используют инверсию (i). В этом случае волновые функции подразделяются на:

четные (симметричные), для которых i [ Ф_g ] = (+1) × Ф_g

нечетные (антисимметричные), для которых i [ Ф_u ] = (–1) × Ф_u

Если волновая функция четная, то все слагаемые, входящие в нее, также должны быть четными. Напротив, нечетная функция может состоять только из нечетных слагаемых. Это позволяет еще более упростить набор неизвестных коэффициентов, подлежащих оптимизации.

Проанализируем пространственную симметрию шести антисимметричных функций, найденных выше. Оператор инверсии меняет местами ядра, что выражается заменой друг на друга символов А и В в выражениях для волновых функций. (На спиновые состояния электронов и описывающие их спиновые функции a и b оператор инверсии не влияет.) Например, для функции Ф₁₃ найдем:

i [ Ф₁₃ ] = i [ Аa × Вb – Вb × Аa ] = [ Вa × Аb – Аb × Вa ] = (– 1) Ф₂₄

Следовательно, функции Ф₁₃ и Ф₂₄ не обладают необходимой пространственной симметрией, они не являются ни четными, ни нечетными. Однако, посредством процедуры симметризации из них можно построить как четную, так и нечетную комбинации.

Рассмотрим сумму:

Ф⁺ = Ф₁₃ + Ф₂₄ = Аa × Вb – Вb × Аa + Аb × Вa – Вa × Аb =

= АВ (ab + ba) – ВА (ab + ba) = [ AB – BA ](ab + ba)

Действуя оператором инверсии на пространственную часть, нетрудно определить, что она является нечетной:

i [ AB – BA ] = [ BA – AB ] = (–1)[ AB – BA ]

Теперь построим разность:

Ф^– = Ф₁₃ – Ф₂₄ = Аa × Вb – Вb × Аa – Аb × Вa + Вa × Аb =

= АВ (ab – ba) + ВА (ab – ba) = [ AB + BA ](ab – ba)

Пространственная часть этой функции является четной:

i [ AB + BA ] = BA + AB = (+1)[ AB + BA ]

Исследование функций Ф₅₇ и Ф₆₈.

Ф₅₇ = Аa × Вa – Вa × Аa = [ АВ – BA ] (aa)

Ф₆₈ = Аb × Вb – Вb × Аb = [ АВ – BA ] (bb)

показывает, что их пространственные множители являются нечетными.

Наконец, проанализируем функции Ф₉ и Ф₁₀.

Ф₉ = Аa × Аb – Аb × Аa = [ AA ] (ab – ba)

Ф₁₀ = Вa × Вb – Вb × Вa = [ BB ] (ab – ba)

Пространственные части этих функций переходят друг в друга при действии пространственных операций симметрии. Следовательно, их также надо подвергнуть процедуре симметризации.

Ф'⁺ = [ AA + BB ] (ab – ba) (четная)

Ф'^– = [ AA – BB ] (ab – ba) (нечетная)

В результате получилось шесть функций, обладающих как перестановочной, так и пространственной симметрией. В перестановочном отношении все они антисимметричны, а в пространственном — распадаются на два класса: четные и нечетные. Суммируем результаты в виде таблицы.

Функ–ция	Выражение через атомные орбитали	Перестановочная симметрия	Пространственная симметрия	S	MS
(Ф^+)u	[AB – BA] (ab + ba)	антисимм.	нечетная
(Ф^–)g	[AB + BA] (ab – ba)	антисимм.	четная
Ф57	[АВ – BA] (aa)	антисимм.	нечетная		+1
Ф68	[АВ – BA] (bb)	антисимм.	нечетная		–1
(Ф'^+)g	[AA + BB] (ab – ba)	антисимм.	четная
(Ф'^–)u	[AA – BB] (ab – ba)	антисимм.	нечетная

В последних двух столбцах указаны значения квантовых чисел — спинового (S) и магнитного спинового (M_S), определяющих величину и ориентацию глобального вектора спина молекулы.

Теперь можно сконструировать три варианта глобальной волновой функции, включающих только однотипные по симметрии слагаемые.

1. Четное синглетное состояние (спин S = 0)

Ф_g = D ₁(Ф^–) + D ₂(Ф'⁺) = { D ₁[ AB + BA ] + D ₂[ AA + BB ]}(ab – ba)

Эта функция содержит два коэффициента (D ₁ и D ₂), из которых неизвестен фактически только один (условие нормировки). Пространственная часть является безузловой и электронное облако не имеет разрывов.

2. Нечетное триплетное состояние спин (S = 1)

Ф_u = F ₁(Ф₅₇) + F ₂ (Ф⁺) + F ₃ (Ф₆₈) =

= [ AB – BA ] { F ₁(aa) + F ₂(ab + ba) + F ₃(bb)}

Функция содержит три коэффициента (F ₁, F ₂ и F ₃), из которых неизвестны только два (условие нормировки). Эти коэффициенты влияют только на ориентацию суммарного вектора спина молекулы, но не на пространственную форму электронного облака. Накладывая внешнее магнитное поле, можно сделать два из этих коэффициентов нулевыми.

3. Нечетное синглетное состояние (спин S = 0)

Ф'_u = Ф'^– = [ AA – BB ] (ab – ba)

В этой функции нет неизвестных коэффициентов. Пространственная часть содержит узел, и электронное облако разделено на две части.

По виду этих волновых функций можно сделать определенные выводы об энергии молекулы. Энергия (без учета магнитных взаимодействий) зависит только от пространственной части волновой функции. Поэтому у молекулы водорода должно быть три энергетических уровня и энергетическая диаграмма должна иметь следующий качественный вид:

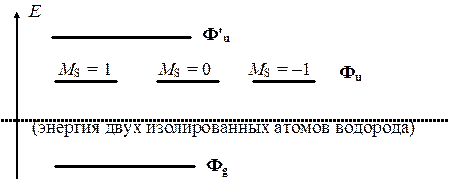
Из диаграммы видно, что два нечетных состояния физически не могут быть реализованы, так как молекула при повышении энергии распадается на отдельные атомы раньше, чем будет достигнуто какое-либо нечетное состояние. Следует подчеркнуть существенный вывод: единственное устойчивое состояние молекулы водорода характеризуется нулевым спином, т.е. электроны в молекуле являются спаренными.

Дата добавления: 2015-07-20