Уравнение непрерывности

Пусть в полупроводнике р-типа в направлении оси x существует положительный градиент концентрации электронов (неосновных но­сителей) dn/dx>0. Такой градиент может быть создан, например, инжекцией электронов с одного концаполупроводника. Предполо­жим далее, что в том же на­правлении х действует электрическое поле напряжен­ности E_x. Выделим в полупроводни­ке слой толщиной dх, рас­положенный перпендикулярно оси х, с площадью попе­речного сечения 1 см² (рис. 6.15). Объем этого слоя ра­вен dх. Обозначим концентрацию электронов в слое в момент времени t через п(х,t), а в момент t+dt через п(х, t+dt). Тогда изменение числа электронов в слое за время dt будет равно:

[n(x,t+dt)-n(x,t)]dx =(∂n/∂t)dtdx. (3.30)

Изменение числа электронов в слое вызывается про­теканием в нем процессов генерации и рекомбинации носителей, а также диффузией и дрейфом носителей, возникающим под действием градиента концентрации и внешнего поля. Рассмотрим каждый из этих факторов в отдельности.

Генерация носителей. За время dt в слое объемом dх ионизирующий фактор создает gdxdt электронов, где g — скорость генерации электронов.

Рекомбинация электронов. Вследствие рекомбинации ежесекундно в единице объема полупроводника уничто­жается R = -(n-n₀)/τ_n электронов. За время dt в объеме dх убыль числа электронов составит: - [(n-n₀)/ τ_n]dxdt.

Рис. 3.3. К выводу уравнения непрерывности.

Диффузия и дрейф носителей. Наличие градиента концентрации и внешнего поля E_x. в направлении оси х приводит к тому, что поток электронов J_п(х), втекаю­щий в слой dх, не равен потоку J_п(х+dх), вытекающему из слоя. Изменение числа электронов в слое за вре­мя dt, вызванное различием этих потоков, составит:

(3.31)

Полное изменение числа электронов в слое за вре­мя dt (уравнение непрерывности для избыточных электронов)будет равно:

(3.32)

Аналогичное уравнение можно получить для избыточных дырок:

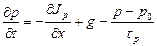(3.33)

При наличии в полупроводнике электрического поля E_x и градиента концентрации электро­нов ток будет складываться из двух составляющих: дрейфовой, обусловленной направленным движе­нием электронов под действием внешнего поля и диффузионой, вызванной диффузией элек­тронов.

Дрейфовый ток. Дрейфовое движение электронов и дырок совершается в струк­туре полупроводника под действием электрического поля и являет­ся направленным. Направленное дрейфовое движение носителей заряда встречает ряд специфических для твердых тел препятствий. Они создаются дефектами структуры и тепловыми колебаниями атомов решетки и примесей. Направленное их движение характеризует подвижность носителей заряда u_i [см²/(В-с)] которая определяется их средней дрейфовой ско­ростью в электрическом поле с напряженностью Е= 1В/см. Подвижность обратно пропорциональна эффективной массе час­тиц. Эффективная масса электронов меньше эффективной массы дырок (т_п*<т_р*) ипоэтому их подвижность больше (u_n>u_p). Для германия u_n/u_p = 3800/1800 ≈2,1 и для кремния u_n/u_p= 1400/500 ≈2,8.

На подвижность носителей заряда в основном влияют два физи­ческих фактора: тепловые колебания атомов кристаллической ре­шетки (рассеяние носителей заряда на тепловых колебаниях ато­мов кристаллической решетки) и электрические поля ионизированных примесей (рассеяние на ионах примесей).

В нижней области рабочего диапазона температур рассеяние вызывается дефектами решетки и атомами примеси. При низкой температуре уменьшаются тепловые скорости движения носителей заряда, увеличивается длительность воздействия электрического поля примеси на носитель заряда и подвижность уменьшается при уменьшении температуры.

В диапазоне больших температур преобладает рассеяние но­сителей заряда на ионах примеси и тепловых колебаниях атомов кристаллической решетки, поэтому с увеличением температуры в этой области подвижность носителей снижается. Рост концентрации носителей сопровождается более частым столкновением частиц, уменьшением длины их свободного пробега и подвижности. Дрейфовый ток равен:

J_Э = nu_n E_x (3.34)

где u_n — подвижность электронов; n — их концентрация.

Электропроводимость. Дрейф электронов и дырок (как разноименных зарядов) под действием электрического поля происходит в противоположных на­правлениях, поэтому суммарная плотность дрейфового тока в крис­талле

I = eE_x (nu_n + pu_p) (3.35)

Коэффициент пропорциональности между напряженностью по­ля E_x и плотностью тока I составляет удельную проводимость

σ = e(nu_n + pu_p) (3.36)

Собственная электропроводимость обусловлена генерацией элек­тронно-дырочных пар, а примесная — ионизацией атомов примеси.

Температурная зависимость удельной проводимости определя­ется главным образом температурной зависимостью концентрации носителей зарядов. Экспоненциальное увеличение концентраций с повышением температуры у собственных по­лупроводников предопределяет такой же характер температурного увеличения собственной проводимости.

В примесном полупроводнике в низкотемпературной области (T<-60°С) степень ионизации примеси мала, поэтому невелика и проводимость. При повышении температуры возрастают ио­низация примеси и проводимость. В рабочем диапазоне темпера­тур (от - 60°С до+100°С) при полной ионизации приме­сей концентрация основных носителей п и р практически постоянна, поэтому проводимость σ_n и σ_p почти не меняется. Некоторое сни­жение проводимости в рабочей области происходит за счет умень­шения подвижности носителей заряда. При температуре Т свыше критической наступает интенсивная тепловая генерация, что вызывает рост концентрации носителей и проводимости и пре­вращение полупроводника в полуметалл.

Фотопроводимость. По­явление в твердом теле избыточных носителей может вызывать свет, падающий на полупроводник. Процесс вну­треннего освобождения носителей под действием света называется внутренним фотоэффектом. Повышение концентрации носителей заряда вследст­вие генерации их светом вызывает повышение проводи­мости полупроводника. Эту дополнительную проводи­мость называют фотопроводимостью в отличие от темновой проводимости, обусловленной тепловым воз­буждением носителей. Возбуждение дополнительных носителей может про­исходить с примесных уровней и из валентной зоны (рис.3.4 ,а). В соответствии с этим различают примесную и собственную фотопроводимости. На рис. 3.4,6 показана схематическая кривая спектрального распределения фотопроводимости. Первый максимум соответствует собст­венной фотопроводимости, два других - примесной фо­топроводимости, обусловленной наличием в полупровод­нике двух типов примесей (рис.3.4 ,а).

Обозначим через Ф интенсивность света, вызывающего переход электронов из валентной зоны в зону проводи­мости, через α коэффициент поглощения света и через β - квантовый выход (число пар носителей, образован­ных одним квантом). Тогда число избыточных носителей, ежесекундно генерируемых в единице объема полупро­водника, будет равно:

g = β α Ф (3.37)

Рис. 3.4. Возбуждение фотоносителей из валентной зоны и примес­ных уровней (а); спектральное распределение фотопроводимо­сти (б).

В отсутствии рекомбинации это число возрастало бы со временем по линейному закону:

Δn_г = β α Фt (3.38)

Вследствие же рекомбинации, скорость которой растет с ростом концентрации избыточных носителей, в полу­проводнике устанавливается стационарное состояние, при котором скорости генерации и рекомбинации уравно­вешивают друг друга. Стационарная концентрация из­быточных носителей будет равна, очевидно, произведе­нию скорости генерации (7.52) на время их жизни τ:

Δn₀ = β α Фτ_n Δp₀ = β α Фτ_p (3.39)

Так как избыточные носители имеют практически такую же подвижность, какой обладают равновесные носители, то стационарная фотопроводимость полупроводника бу­дет равна:

σ_Ф = eβ α Ф(u_nτ_n + u_pτ_p) (3.40)

Диффузионный ток. Ток, обусловленный диффузией электронов, пропор­ционален градиенту их концентрации:

J_D = D_п(∂п/∂х) (3.41)

Коэффициент пропорциональности D_n называется коэф­фициентом диффузии.

Полный ток, обусловленный движением электронов, равен:

J_n = nu_n E_x + D_п(∂п/∂х) (3.42)

Аналогичное выражение можно получить для тока, обусловленного движением дырок:

J_p = nu_p E_x + D_p(∂p/∂х) (3.43)

Знак минус у диффузионной составляющей указывает на то, что диффузионный ток дырок направлен противо­положно градиенту их концентрации (в сторону умень­шения концентрации дырок).

Связь между изменением концентрации носителей в элементарном объеме полупроводника и током, проходящим через этот объем, устанавливается уравнением непрерывности

(3.44)

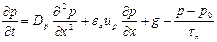(3.45)

В стационарных условиях концентрация электронов и дырок не меняется со временем (∂n/∂t=0 и ∂p/∂t = 0) и уравнение непрерывности приобретает следующий вид:

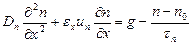(3.46)

(3.47)

Эти уравнения выражают закон сохранения числа ча­стиц: в стационарных условиях поток частиц, вытекаю­щий из единицы объема полупроводника, равен числу частиц, генерируемых в этом объеме внешним ионизи­рующим фактором, за вычетом числа частиц, рекомбинирующих в этом объеме.

3.4. Соотношения Эйнштейна и диффузионная длина

Дрейфовый ток в полупроводнике может возникнуть и без приложения внешнего поля. Рассмотрим, напри­мер, полупроводник п -типа с неравномерным распределением донорной примеси вдоль его длины, которую направим по оси х (рис. 3.5). В таком полупроводни­ке возникает диффузионный ток электронов, обусловлен­ный переходом их из обла­стей с большей концентраци­ей в область с меньшей кон­центрацией.

Перетекание электронов приводит к появ­лению нескомпенсированных объемных зарядов: в местах полупроводника откуда электроны уходят, в результате возникает нескомпенсированный по­ложительный заряд ионизированных доноров, места же полупроводника с низкой концентрацией доноров, в ко­торые перетекают электроны, заряжаются отрицательно. Образование объемных зарядов сопровождается возникновением электрического поля и появлением дрейфового тока, направленного противоположно диф­фузионному току. Диффузионный перенос электронов будет происходить до тех пор, пока диффузионный и дрейфовый токи не уравняются:

nu_n E_x = - D_n(∂n/∂х)

Рис.3.5. Возникновение диффузионного и дрейфового токов в полупроводнике при наличии градиента кон­центрации примеси.

Выразив концентрацию электронов в области, охватывающей точку х, в соответствии с за­коном распределения Больцмана в условиях равнове­сия и продиференцировав (6.98) по х, получим:

(3.48)

Аналогичное выражение можно получить для коэф­фициента диффузии дырок:

(3.49)

Формулы (6.100) и (6.101) называются соотноше­ниями Эйнштейна. Они связывают коэффициенты диф­фузии заряженных частиц с их подвижностью.

Диффузионная длина. Кроме времени жизни и коэффициента диффузии явление рекомбинации можно характеризовать так называемой диффузионной длиной. Эта величина по определению представляет расстояние, на котором концентрация неравновесных носителей уменьшается в е раз. Очевидно, что это расстояние определяется временем жизни и коэффициентом диффузии носителей.

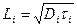(3.50)

Смысл диффузионной длины ясен из предыдущего:– это среднее расстояние, на которое диффундирует носитель за время своей жизни. Зная диффузионную длину L и коэффициент диффузии D, можно по формулам вычислить время жизни носителей τ.

Для германия D_n = 0,0092 м²/с D_p = 0,0044 м²/с

Для кремния D_n = 0,0035 м²/с D_p = 0,0012 м²/с

---

Дата добавления: 2015-07-25