Зонная структура энергетического спектра носителей заряда

Московский Государственный Университет Приборостроения и Информатики

Е.Н. ВИГДОРОВИЧ

Физические основы

И технология электронных средств

Учебное пособие

Часть 1

«Физические основы»

Москва

МГУПИ 2008 год

621.3

УДК 621.382 Утверждено Ученым Советом

в качестве учебного пособия

Физические основы и

технология электронных средств

Учебное пособие

М. Изд. МГАПИ, 2008

Под редакцией

проф. Рыжикова И.В.

Учебное пособие содержит краткий материал по физическим основам процессов формирования свойств электронных средств.

Пособие предназначено для преподавателей, инженерно-технических работников и студентов различных специальностей

______________________________

@ Московская государственная академия приборостроения и информатики, 2005

1. ЭНЕРГЕТИЧЕСКИЙ СПЕКТР НОСИТЕЛЕЙ ЗАРЯДА

Зонная структура энергетического спектра носителей заряда

Стоящая перед нами задача сводится к рассмотрению свойств и поведения заряженных частиц в кристаллическом твердом теле.

Из курсов атомной физики и квантовой механики известно пове­дение электронов в отдельно взятом изолированном атоме. В этом случае электроны могут обладать не любыми значениями энергии Е, а лишь некоторыми. Энергетический спектр электронов приобретает дискретный характер, как это показано на рис. 1.1, в. Переходы с од­ного энергетического уровня на другой связаны с поглощением или выделением энергии.

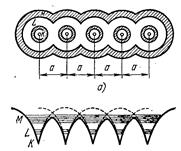
б) в) г)

Рис. 1.1. Схема образования энергетических зон в кри­сталлах:

а — расположение атомов в одномерном кристалле; б — распре­деление внутрикристаллического потенциального поля; в — рас­положение энергетических уровней в изолированном атоме; г — рас­положение энергетических зон

Возникает вопрос, как изменятся энергетические электронные уровни в атомах, если приближать атомы друг к другу, т. е. конден­сировать их в твердую фазу. Упрощенная картина такого одномер­ного кристалла приведена на рис. 1.1, а.

Качественный ответ на этот вопрос получить нетрудно. Рассмотрим какие силы действуют в отдельном атоме, и какие — в кристалле. В изолированном атоме существуют сила притяжения ядром атома всех своих электронов и сила отталкивания между электронами. В кристалле из-за близкого расстояния между атомами возникают новые силы. Это — силы взаимодействия между ядрами, между элек­тронами, принадлежащими разным атомам, и между всеми ядрами и всеми электронами. Под влиянием этих дополнительных сил энергетические уровни электронов в каждом из атомов кристалла каким-то образом должны измениться. Одни уровни понизятся, другие повысятся на шкале энергий. В этом состоит первое следствие сближения атомов. Второе следствие связано с тем, что электронные оболочки атомов, в особенности, внешние могут не только соприкасаться друг с другом, но спо­собны даже перекрыться. В результате этого электрон с одного уровня в каком-либо из атомов может перейти на уровень в соседнем атоме без затраты энергии и, таким образом, свободно перемещаться от одного атома к другому. В связи с этим нельзя утверждать, что данный электрон принадлежит какому-нибудь одному определенному атому, наоборот, электрон в такой ситуации принадлежит всем атомам кри­сталлической решетки одновременно. Иными словами, происходит обобществление электронов. Разумеется, что полное обобществление происходит лишь с теми электронами, которые находятся на внешних электронных оболочках. Чем ближе электронная оболочка к ядру, тем сильнее ядро удерживает электрон на этом уровне и препятствует перемещению электронов от одного атома к другому.

Совокупность обоих следствий сближения атомов приводит к по­явлению на энергетической шкале вместо отдельных уровней целых энергетических зон (рис. 1.1, г), т. е. областей таких значений энер­гий, которыми может обладать электрон, находясь в пределах твер­дого тела. Ширина зоны должна зависеть от степени связи электрона с яд­ром. Чем больше эта связь, тем меньше расщепление уровня, т. е. тем уже зона. В изолированном атоме имеются запрещенные значения энергии, которыми не может обладать электрон. Естественно ожи­дать, что нечто аналогичное будет и в твердом теле. Между зонами (теперь уже не уровнями) могут быть запрещенные зоны. Характерно, что если в отдельном атоме расстояния между уровнями будут не­велики, то в кристалле запрещенный участок может исчезнуть за счет перекрытия образующихся энергетических зон.

Таким образом, энергетический спектр электронов в кристалле имеет зонную структуру.. Количественное решение задачи о спектре электронов в кристалле с помощью уравнения Шредингера так же приводит к выводу, что энергетический спектр электронов в кристалле имеет зонную структуру. Интуитивно можно представить, что раз­личие в свойствах разных кристаллических веществ однозначно свя­зано с разной структурой энергетического спектра электронов (раз­ная ширина разрешенных и запрещенных зон)

Квантовая механика для объяснения ряда свойств материи рассматривает эле­ментарные частицы, в том числе и электрон одновременно и как частицу, и как некую волну. Т. е. электрон можно одновременно характеризовать величинами энергии Е и импульса р, а также длиной волны λ, частотой ν и волновым вектором k = р/h. При этом, Е=hν и p = h/λ. Тогда движение свободных электронов может быть описана плоской волной, именуемой волной де-Бройля, с постоянной амплитудой.

Дата добавления: 2015-07-25