Функция распределения Ферми—Дирака

Если частицы подчиняются принципу Паули (например, электроны, нейтроны и др.), то в каждом энергетическом состоянии одновременно не может быть более одной частицы. В этих условиях функция распределения, выражающая среднее число частиц в данном энергетическом состоянии, будет представлять собой вероятность заполнения данного состояния. Расчетом наиболее вероятного распределения по энергетическим уровням неразличимых частиц, подчиняющихся принципу Паули, получают формулу ·

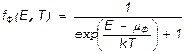(2.4.)

получившую название функции распределения Ферми—Дирака. Частицы, описываемые этой функцией распределения, получили; название фермионов.

Рассмотрим основные свойства распределения Ферми—Дирака применительно к электронам в металле. При температуре абсолютного нуля электроны последовательно занимают все состояния, начиная с самого нижнего, соответствующего дну зоны проводимости. Значение функции распределения для всех этих уровней, очевидно, равняется единице. Как видно из формулы (2.4.),. последним заполненным состоянием будет энергетический уровень, высота которого, отсчитанная от дна зоны проводимости, равна химическому потенциалу Е_F = μ_Ф. Этот энергетический уровень Е_F полу­чил название уровня Ферми. Все энергетические уровни, лежащие выше уровня Ферми, свободны, а значение функции распределения для этих уровней равно нулю (f_Ф(Е>E_F) = 0). Описанное распределе­ние электронов по энергиям при Т = 0°К показано на рис.2.3 ,а ступенчатой линией.

При повышении температуры часть электронов переходит на более высокие энергетические уровни Е > Е_F, в результате чего вероятность заполнения этих уровней увеличивается, а вероятность заполнения уровней, лежащих ниже уровня Ферми Е <E_F, уменьшается. Ход кривых функции распределения для двух значений температуры, отличных от нуля, показан кривыми на рис. 2.3,а.

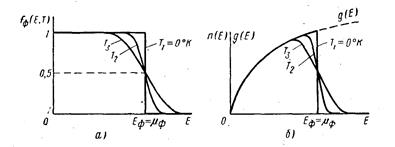
Рис. 2.3. Графики функции распределения Ферми — Дирака (а) и распределение частиц по энергиям (б) при трех различных значениях

температуры

С учетом введенного понятия об уровне Ферми функция распреде­ления Ферми—Дирака запишется так:

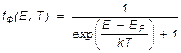(2.5.)

Из формулы (2.5) следует важное свойство уровня Ферми: вероят­ность заполнения электроном уровня E_F при любой температуре равна 1/2.

Графики полученного распределения электронов для трех значений температуры показаны на рис. 2.4,6.

На рис.2.4. для сравнения приведены различные кривые распределения электронов.

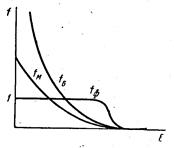
Рис.2.4. Кривые распределения Максвелла-Больцмана (f_M) Бозе-Эйнштейна (f_Б) и Ферми –Дирака (f_Ф)

Видно, что значения функций распределения при малых энергиях в случае статистики Максвелла-Больцмана и Бозе-Эйнштейна значительно больше, чем в случае статистики Ферми-Дирака. Следует, однако, отметить, что при

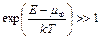(2.6.)

статистики Бозе-Эйнштейна и Ферми-Дирака переходят в статистику Максвелла-Больцмана, которую можно рассматривать как предельный случай этих двух квантовых статистик. Исходя из выше изложенного видно что в оптоэлектронике необходимо использовать распределение Бозе-Эйнштейна, а в микроэлектронике распределение Ферми-Дирака.

Электронный газ, подчиняющийся распределению Ферми — Дирака, принято называть вырожденным, а величину приведенного уровня Ферми 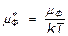— степенью вырождения. Разумеется, что деление на вырожденный и невырожденный газы в значительной степени условно, ибо нельзя провести четкую границу между ними. Тем не менее, в качестве такой границы было принято значение μ_Ф = -2. При μ_Ф > -2 электронный газ будет вырожденным, а при μ_Ф < -2 — невырожденным.

2.4. Концентрация носителей заряда

В общем случае концентрация свободных носителей заряда в кри­сталле может быть вычислена интегрированием произведения плот­ности квантовых состояний g(E) на функцию распределения f_F(E) по всем энергетическим уровням системы в соответствии с формулой.

n(E)dE=f(E,T)g(E)dE

Для определения концентрации электронов в зоне проводимости интегрирование следует производить от уровня дна зоны проводимости Е_с до верхнего уровня Е_так. Поскольку функция распределения быстро уменьшается с ростом энергии, то значение верхнего предела интегрирования без заметной погрешности расчета может быть сколь угодно увеличено или взято равным бесконечности. После интегрирования получим

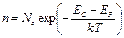(2.7.)

где N_C –эффективная плотность состояний в зоне проводимости.

Для концентрации дырок можно вывести аналогичное уравнение

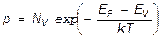(2.8.)

где N_V –эффективная плотность состояний в валентной зоне.

Собственный полупроводник. Полученные формулы для концентраций электронов и дырок являются справедливыми как для собственного, так и для слаболегированного полупроводника. Существенная разница, однако, при · этом заключается в положении уровня Ферми. Найдем положение уровня Ферми и концентрацию носителей заряда для собственного? полупроводника.

Положение уровня Ферми в однородном кристалле определяется. из условия нейтральности. Дело в том, что в состоянии равновесия · уровень Ферми всех частей системы должен быть одинаков. В случае собственного или однородно легированного полупроводника постоянство уровня Ферми обусловлено отсутствием объемного заряда. Если'' по каким-либо причинам в таком полупроводнике возникнет объемный заряд, который приведет к изменению положения уровня Ферми, то создаваемое этим зарядом электрическое поле вызовет, такое перемещение электронов и дырок, которое компенсирует объемный заряд и восстановит исходный уровень Ферми.

В собственном полупроводнике условие нейтральности, позволяю­щее найти уровень Ферми, определяется равенством концентраций электронов и дырок p=n. Из этого равенства находится формула для уровня Ферми в собственном полупроводнике:

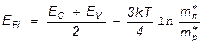(2.9.)

Нетрудно видеть, что в собственном полупроводнике уровень Ферми проходит вблизи середины запрещенной зоны, причем величина смещения его в ту или иную сторону от середины зависит от отношения эффективных масс электрона и дырки. Если полученную формулу для уровня Ферми подставить в (2.7) и (2.8), то найдем концентрацию носителей заряда в собственном полупроводнике:

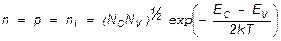(2.10.)

При комнатной температуре в беспримесном германии n_i = 2,37.10¹³см^-3, а в беспримесном кремнии n_i = 1,38.10¹⁰ см ^-3.

Легированный полупроводник. Если в полупроводнике содержатся примеси или дефекты, обра­зующие донорные или акцепторные уровни в запрещенной зоне, то появляются дополнительные электронные переходы, изменяющие концентрацию носителей заряда и положение уровня Ферми. Кон­центрация электронов в зоне проводимости и дырок в валентной зоне в этом случае описывается теми же выражениями (2.7) и (2.8), однако энергия уровня Ферми уже не определяется формулой (2.9), а яв­ляется функцией концентрации примесей. При определении положе­ния уровня Ферми в этом случае надо учитывать не только свободные носители заряда, но и электроны на акцепторных уровнях п_A и дырки на донорных уровнях р_D. Степень заполнения примесных уровней по-прежнему определяется функцией Ферми—Дирака. Если концент­рация примесей невелика, то их энергетический уровень является дискретным. В этом случае концентрация носителей заряда на примесных уровнях находится перемножением величины концентрации примесных атомов на значение функции Ферми—Дирака, которое она имеет на примесном уровне. Поэтому если энергии уровней акцеп­торов и доноров обозначить через Е_A и E_D, а их концентрации — соот­ветственно через N_A и N_D, то концентрации электронов на акцептор­ных уровнях п_A и дырок на донорных уровнях р_D могут быть выра­жены формулами:

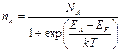(2.11.)

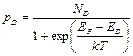(2.12.)

В общем случае условие электрической нейтральности требует чтобы полная концентрация электронов равнялась полной концентрации дырок: -

n + n_A = p + p_D

В случае электронного полупроводника, в котором имеются только донорные уровни, при сравнительно низких температура когда переходы осуществляются только с донорных уровней в зону проводимости, концентрация дырок в валентной зоне ничтожно мала по сравнению с концентрацией свободных электронов (п > р). Поэтому условие нейтральности упрощается и приобретает вид n = р_D. При равнивая (2.7) и (2.12), получим выражение для уровня Ферми в случае электронного полупроводника:

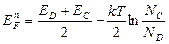(2.13.)

Если подставить полученное выражение в формулу (2.7) для концентрации электронов, то получим:

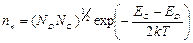(2.14.)

Представляет определенный интерес нахождение концентрации неосновных носителей — дырок р_n в электронном полупроводнике. Для этого необходимо выражение для уровня Ферми (2.13) подставить в (2.8). После простых преобразований получим

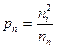(2.15.)

Найденное выражение устанавливает простую связь между концентра­цией основных и неосновных носителей заряда:

n_n p_n = n_i ² (2.16.)

и доказывает, что произведение этих концентраций не зависит от по­ложения уровня Ферми и концентрации примеси, а определяется лишь температурой.

Найденная зависимость (2.16) обусловливается термодинамиче­ским равновесием в полупроводнике и называется законом действующих масс. Из этого закона следует, что с повышением кон­центрации донорной примеси и, следовательно, с ростом концентрации основных носителей наблюдается при постоянной температуре пропорциональное уменьшение концентрации неосновных носителей так, что их произведение остается постоянным и равным квадрату концентрации электронов в чистом полупроводнике. Закон действую­щих масс справедлив для любого невырожденного полупроводника в условиях термодинамического равновесия.

Рассмотрим далее поведение концентрации основных носителей при увеличении температуры. С повышением температуры концент­рация электронов в электронном полупроводнике возрастает до тех пор, пока не приблизится к концентрации доноров. Условием ней­тральности полупроводника в этом случае будет равенство п_n = N_D. Подставляя в это равенство выражение для концентрации электро­нов (2.8), после несложных преобразований получим формулу для уровня Ферми в рассматриваемом температурном диапазоне:

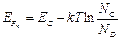(2.17.)

Дальнейшее повышение температуры приводит к увеличению концентрации электронов проводимости за счет возбуждения их из валентной зоны. При этом наблюдается соответствующее увеличение и концентрации дырок. Если концентрация дырок в валентной зоне, возникших за счет возбуждения электронов в зону проводимости, значительно превысит концентрацию доноров N_D то полупроводник по своим свойствам оказывается близким к беспримесному. Действи­тельно, при этом концентрация электронов равна концентрации ды­рок, которая описывается формулой (2.10), уровень Ферми смещается в среднюю часть запрещенной зоны, совпадает с уровнем Ферми для беспримесного полупроводника и определяется формулой (2.9).

Аналогичные зависимости наблюдаются и в дырочном полупро­воднике, в котором имеются только акцепторные уровни. При низ­ких температурах концентрация дырок в валентной зоне равна числу электронов, перешедших на акцепторные уровни п_A. Выражение для уровня Ферми определяется, как и в предыдущем случае, из усло­вия n_A = p_P..

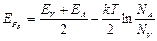(2.!8.)

Подставляя найденное выражение для уровня Ферми в (2.8), получим формулу для концентрации дырок в дырочном полупроводнике:

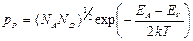(2.19.)

Концентрация неосновных носителей электронов может быть найдена по закону действующих масс:

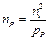(2.20.)

Как и в случае электронного полупроводника, с повышением тем­пературы в дырочном полупроводнике наступает такой момент, когда все акцепторы окажутся ионизированными, а концентрация дырок будет равна концентрации акцепторов р_P = N_D. Уровень Ферми в этом случае определяется как:

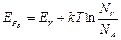(2.21.)

Концентрация неосновных носителей — электронов — определяется в этом случае также по закону действующих масс.

При дальнейшем повышении температуры концентрация дырок начинает возрастать за счет переходов электронов из валентной зоны в зону проводимости. С момента, когда концентрация электронов в зоне проводимости, вы­званная этими переходами, окажется значительно боль­ше концентрации акцепто­ров, дырочный полупро­водник начинает вести себя как беспримесный.

Если в образце имеются оба сорта примесей — доноры и акцеп­торы, то тип проводимости определяется по преобладающей примеси. Если, например, концентрация доноров N_D больше концентрации ак­цепторов N_A,то при Т = 0 К все акцепторные уровни будут запол­нены электронами, перешедшими с доноров. Условием нейтральности в этом случае будет

N = p_D –N_A

где концентрация ионизированных доноров р_д по-прежнему опреде­ляется формулой (2.12), а концентрация свободных электронов выра­жается формулой (2.7). При повышении температуры все донорные уровни опустошатся и концентрация электронов станет постоянной и равной разности числа доноров и акцепторов:

n = N_D –N_A (2.22.)

Аналогичные закономерности наблюдаются в дырочном полупро­воднике, содержащем некоторое количество доноров.

Обычно в полупроводнике всегда имеется большее или меньшее количество неосновной примеси, т. е. доноров в дырочном полупровод­нике и акцепторов в электронном полупроводнике. Отношение числа неосновных центров к основным (N_D/N_A или N_A/N_D. соответственно) называют степенью компенсации, а образцы, содержа­щие оба вида центров, — компенсированными.

---

Дата добавления: 2015-07-25