Заполнение зон. Эффективная масса носителей заряда

До сих пор рассматривались возможные значения энергии электро­нов и было установлено, что все энергетические уровни, которыми могут обладать электроны, расположены в зонах. Возникает вопрос - все ли из возможных уровней в действительности заняты электронами? Т. е. каково заполнение зон?

Качественно этот вопрос можно проанализировать, если вспомнить каково же заполнение энергетических уровней в изолированном атоме. Так как в нейтральном изолированном атоме внутренние энерге­тические уровни полностью заполнены, а не полностью заполненным может быть лишь крайний валентный уровень, то и заполнение зон в кристалле оказывается различным. Зоны, произошедшие от внутрен­них уровней, всегда полностью заполнены электронами. Только зона, образованная от валентных уровней, может ока­заться в ряде случаев заполненной не полностью. Зону, произошедшую от валентных уровней атомов, образующих кристалл, называют валентной зоной.

Степень заполнения валентной зоны электронами зависит, прежде всего, от химической природы атомов, из которых состоит кристалл, определяемой величиной Z, от кристаллической структуры и от мно­гих других: более тонких факторов. В случае одноатомных кристаллов с простой структурой, т. е. с базисом, состоящим из одного атома, полное число электронов в кри­сталле будет NZ где N — число атомов в кристалле a Z - число электронов, приходящихся на один атом (атомный номер). Число же квантовых состояний в каждой отдельной -разрешенной зоне равно 2N

Тогда количество заполненных электронами зон будет NZ/2N = = Z/2. Таким образом, если Z нечетно, то заполненным оказывается нецелое число зон. Т.е. элементы с нечетным атомным номером, если они кристаллизуются в простой решетке, будут иметь не полностью заполненную зону, произошедшую от валентных уровней. Из дальнейшего изложения станет ясно, что обратное утверждение о том, что у элементов с четным Z эта зона должна быть запол­нена полностью, не пра­вильно.

В изолированном ато­ме выше валентного уровня находятся уров­ни энергии, на которых хотя электронов и нет, но они могут там нахо­диться при возбуждении атомов. Для этого ва­лентному электрону не­обходимо преодолеть энергетический барьер, равный потенциалу воз­буждения атома. Точно так же и в кристалле выше валентной зоны имеется полностью сво­бодная от электронов зона, которую называют зоной проводимости. За­полнение зоны проводимости может начаться только если электроны в валентной зоне получат дополнительную энергию, достаточную для преодоления энергетического барьера, равного ширине запре­щенной зоны, лежащей между валентной зоной и зоной проводимости.

Изобразим теперь возможные случаи зонной структуры с учетом·; степени заполнения зон. Таких случаев может быть четыре (рис. 1.2).

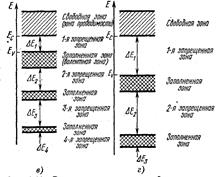
Рис. 1.2. Возможные случаи зонной структуры твердых тел:

б — металл, состоящий· из одновалентных атомов; б — ме­талл, состоящий из двухвалентных атомов; в — полу­проводник; г — полупроводник с большой величиной запрещенной зоны (диэлектрик)

Случай а. Валентная зона заполнена не полностью. При при­ложении к такому кристаллу электрического поля электроны будут получать от него энергию и будут, соответственно, переходить на более высокие энергетические уровни. Из рис. 1.2, б видно, что во всех глубоко лежащих зонах этот процесс невозможен, так как в глу­боких зонах все уровни полностью заняты.. Валентная зона заполнена лишь частично и в ней переходы электронов будут происходить беспре­пятственно, что обеспечивает прохождение электрического тока через такой кристалл при любой температуре. Здесь, таким образом, случай хорошо проводящего ток кристалла, электропроводность которого не меняется с температурой, т. е. это случай описывает свойства металла.

Случай б. Валентная зона заполнена полностью, но запрещен­ная зона между валентной зоной и зоной проводимости отсутствует (рис. 1.2, б). Такой кристалл опять-таки будет хорошо проводить электрический ток и его электропроводность также не будет зависеть (или почти не будет· зависеть) от температуры. Таким образом, и этот случай соответствует металлическому кристаллу. Отличие от случая а заключается в том, что в отдельных атомах, из которых образуется этот металл, валентные уровни за­полнены полностью, но ближайшие к валентным уровни находятся на столь близких расстояниях, что при образовании зон, валентная зона и зона проводимости оказываются перекрывшимися друг с дру­гом.

Случай в и г. Валентная зона заполнена полностью и не пе­рекрыта с зоной проводимости (рис. 1.2, в и 1.2, г). Это случаи, когда перемещение электронов под действием электрического поля не может происходить до тех пор, пока каким-либо способом, например нагревом, не будет переведена часть электронов из валентной зоны в зону проводимости. Т. е. эти случаи описывают кристаллы, электро­проводность которых должна повышаться с увеличением температуры. Такие кристаллы называют полупроводниками. Различие случаев в и г лишь в величинах запрещенных зон. Со­вершенно очевидно, что для преодоления большего энергетического зазора (рис. 1.2, г) потребуется и более высокая температура. Поэ­тому кристаллы, у которых проводимость возникает при очень вы­соких температурах, принято относить к диэлектрикам. Условно при­нято считать, что кристаллы такого типа будут диэлектриками, если ши­рина запрещенной зоны будет больше 2 эВ (46,12 ккал/г-моль). Хотя с физической точки зрения и такие кристаллы являются полу­проводниками.

Анализ степени заполнения зон позволяет в дальнейшем исклю­чить из рассмотрения все глубокие зоны, лежащие ниже валентной, так как электроны в этих зонах не участвуют в прохождении электри­ческого тока через кристалл. Таким образом, зонную структуру, которую рассмотрим в дальнейшем, будем изображать так, как она показана на рис. 1.3.

Рис.1.3. Упрощенная схема зонной энергетической структуры

Обычно принято для краткости изображать лишь потолок валентной зоны, обозначаемый Е_υ подразумевая, что сама валентная зона располагается ниже этого уровня. Точно так же принято изображать дно зоны проводимости, т. е. ее нижний уровень, обоз­начаемый е_с. Ширину запрещенной зоны принято обозначать E_g.

Как уже говорилось выше, проводимость в полупроводнике воз­никает только после того, как часть электронов будет переброшена из валентной зоны в зону проводимости. Этот процесс показан на рис. 1.3 пунктиром. После этого валентная зона оказывается уже не полностью заполненной и в ней также станет возможным перемеще­ние электронов, т. е. повышение их энергии при приложении электри­ческого поля. Таким образом, механизм протекания электрического тока через рассматриваемый кристалл обусловлен одновременным перемещением электронов и в зоне проводимости, и в валентной зоне. Разумеется, что такое перемещение должно отличаться от движения действитель­но свободных электронов в вакууме, так как в кристалле на электроны действует еще и внутреннее периодическое потенциальное поле. Привычным является описание движения тел в рамках классической механики Ньюто­на, которая устанавливает связь между внешней силой F, приложенной к телу, и его ускорением. В кристалле же на электрон действует периодическое поле, явившееся следствием действия на электрон многих внутренних сил. Эти силы также должны учитываться величиной F. Поэтому рассчитать истинную траекторию электрона в кристалле не представляется возможным, так как нельзя точно решить задачу действия многих сил. Да если такую задачу и удалось бы решить, то законы действия этих сил оказались бы не столь наглядными в сравнении с ньютоновской механикой. Неприменимость ньютоновской механики для электронов доказывают обычно на основании известного в квантовой механики принципа неопределенности, при котором неопределенность в величине скорости электрона оказывается больше самой скорости, что, конечно, является абсурдом. Таким образом, для электрона в кристалле понятие о мгновенной скорости теряет смысл. Остается лишь понятие о средней скорости электрона.

Чему же равна средняя скорость электрона в кристалле? Ее можно определить как групповую скорость волн, с помощью которых опи­сывается электрон;

(1.1.)

За время dt внешняя сила F совершает работу по перемещению электрона, численно равную

(1.2)

Отсюда находим

(1.3.)

Дифференцируя v_Г по времени получим ускорение электрона в виде

(1.4.)

Сравнивая это выражение с законом Ньютона для обычных тел можно увидеть полное сходство, если трактовать как аналог массы величину

(1.5.)

Эту величину называют эффективной массой. Смысл введения эффективной массы заключается в том, что с ее помощью учитывают совместное действие периодического потенци­ального поля и внешней силы на электрон в кристалле. Посредством введения эффективной массы удалось сложные законы движения электронов в кристалле свести к законам, которые по форме (только по форме!) совпадают с хорошо известными законами классической механики. Следует понимать, что эффективная масса ничего общего не имеет с обычной массой, т. е. она не является мерой инерции и не связана с силами тяготения. Более того Е является переменной величиной в зависимости от k, а значит, и – d²E/dk² может быть переменной величиной, т. е. эффективная масса может быть не постоян­ной в отличие от обычной истинной массы электрона.

Таким образом, эффективная масса есть лишь коэффициент про­порциональности в законе, связывающем внешнюю силу, действующую на электрон в кристалле с его ускорением.

Возвращаясь к описанию перемещения электронов в зонах приходим к необходимости описывать его дви­жением электронов в зоне проводимости с хотя и переменной по величине, но все-таки с нор­мальной положительной эффективной массой и одновременно - движением электронов с ано­мальной - отрицательной массой в валентной зоне.

Во избежание трудностей при описании такого движения было введено понятие положительной дырки, перемещение которой в электрическом поле происходит в противоположном направлении по сравнению с электроном. Тогда масса такой положительной дырки положительна. Движение электрона в валентной зоне носит характер эста­феты: электрон переходит на верхний свободный уровень и остается на нем, на освободившийся уровень приходит электрон с еще более низкого уровня и т. д. При таких перемещениях электронов, про­исходящих вверх по шкале энергий, освобождающийся энергетиче­ский уровень движется вниз в глубь валентной зоны. Поэтому про­тивоположно направленные движения электрона и освобождающегося уровня в валентной зоне эквивалентны. Освобождающийся уровень и отождествляется с некой фиктивной частицей, которая имеет равный по величине, но противоположный по знаку заряд по сравнению с электроном. Эта частица и есть дырка. Дырки с меньшей энергией располагаются у потолка валентной зоны и увеличивают свою энер­гию, перемещаясь по шкале энергий вглубь валентной зоны. Иными словами, для дырок и электронов отсчет энергий идет в противопо­ложных направлениях. Энергетический спектр Е (k) приобретает вид, изображенный на рис. 1.4.

Рис. 1.4. Энергетический спектр электронов и дырок в коорди­натах Е — k

Дата добавления: 2015-07-25