Читайте также:
|
В классической физике частицы предполагаются различимыми, причем в данном энергетическом состоянии может находиться неограниченное число классических частиц. Примером таких классических частиц является молекулярный газ. Эти частицы описываются хорошо известной в классической физике функцией распределения Максвелла— Больцмана:
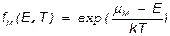(2.1.)
где μМ - представляет собой термодинамический параметр, называемый химическим потенциалом. Химический потенциал выражает изменение свободной энергии системы при изменении числа частиц этой системы на единицу, при неизменных температуре и объеме системы. Иными словами, химический потенциал равен величине свободной энергии; приходящейся на одну частицу системы в состоянии равновесия, и выражается формулой
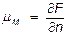(2.2.)
где n –число частиц в системе
На рис.2.1. приведены графики функции распределения при трех различных значениях температуры. Как видно из рисунка, с уменьшением температуры число частиц с малыми значениями энергии неограниченно возрастает. При температуре абсолютного нуля все частицы займут самое нижнее энергетическое состояние.
Рис.2.1. Графики функции распределения Максвелла-Больцмана (а) и распределение частиц по энергиям (в) при трех различных значениях температуры.
Дата добавления: 2015-07-25; просмотров: 183 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дефекты в кристаллах | | | Функция распределения Бозе - Эйнштейна |