Определение оценок параметров закона Вейбулла

Оценка параметров масштаба а, формы b и сдвига с методом моментов осуществляется по выборке независимых наблюдений случайной величины X. Определение производится по значению коэффициента асимметрии с помощью специальных таблиц, в следующем порядке:

вычисляют оценку коэффициента асимметрии по формуле:

(4.8)

для группированных данных оценку коэффициента асимметрии ρВ вычисляют по формуле:

(4.9)

- по полученному значению ρВ из таблицы Б4 приложения Б при помощи линейной интерполяции находим оценку параметра b и значения коэффициентов gb и Kb;

- определяем оценку для параметра а по формуле:

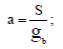(4.10)

- находим значение c по формуле:

(4.11)

в качестве оценки параметра с берут одно из двух значений:

(4.12)

Пример 7 Определим оценки параметров закона Вейбулла для данных из примера 2.

Вычислим значение коэффициента асимметрии по формуле (4.9):

ρb = (1/45)((91,7-242,8)³·1+…+(308,2-242,8)³·9)/60,48³ = 0,826.

По таблице Б4 приложения Б с помощью линейной интерполяции находим значения оценок параметра b и значения коэффициентов gb и Kb.

Интерполяцию будем производить по схеме Эйткина. По зависимости значений параметра формы от коэффициента асимметрии в двух точках

ρb0 = 0,865, b0 =1,70,

ρb1 = 0,779, b1 = 1,80,

взятых так, что ρb0 > ρb > ρb1.

Найдем с помощью схемы Эйткина значение b для ρb = 0,83 с помощью формулы:

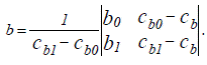(4.13)

Аналогичным образом находим значения коэффициентов gb и Kb:

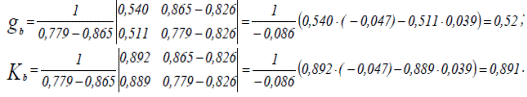
Определим значение параметра а:

a = 60,48/0,527 = 114,76.

Находим значение c:

c = 201,8 – 114,76·0,891 = 99,55.

Так как 99,55 > 70, принимаем с = 70.

Дата добавления: 2015-10-16