Определение оценок параметров экспоненциального закона

Оценка параметра распределения, л, находится по формуле:

л = 1 / Х, (4.3)

где Х - оценка математического ожидания выборки.

Определение оценок параметров нормального закона

Оценка параметра m_t, представляющего собой среднее значение случайной величины t, равна оценке математического ожидания выборки.

Оценка параметра σ равна оценке среднего квадратического отклонения выборки.

Определение оценок параметров логарифмически нормального

Закона

Параметр μ вычисляется по формуле:

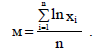(4.4)

Параметр S вычисляется по формуле:

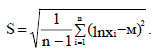(4.5)

В случае больших выборок параметр μ вычисляется по формуле:

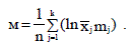(4.6)

Параметр S вычисляется по формуле:

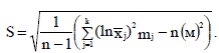(4.7)

Пример 6 Определим оценки параметров логарифмически-нормального закона для данных из примера 1.

Найдем оценку параметра μ с помощью формулы (4.4):

μ = (ln13 + ln 27 + … + ln 44)/15 = 53,96/15 = 3,6.

Оценку параметра S можно найти с помощью формулы (4.5). На практике, для облегчения расчетов, используют соотношение примера 1. Таким образом, оценку дисперсии проще найти по формуле:

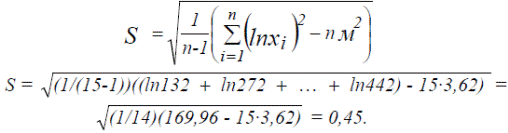
Определим оценки параметров логарифмически-нормального закона для данных из примера 2.

Найдем оценку параметра μ с помощью формулы (4.6):

μ = (ln91,7·1 + ln135·1 + … + ln308,2·9)/45 = 5,41.

Найдем оценку параметра S по формуле (4.7):

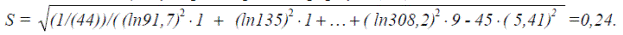
Дата добавления: 2015-10-16