Интервальные оценки

Интервальные оценки - это оценки, которые с доверительной вероятностью γ в некотором интервале содержат истинное значение числовой характеристики:

Р (и <и<и) = γ, (2.9)

где и и и - соответственно нижняя и верхняя доверительные границы

интервала значений оцениваемой характеристики;

θ – истинное значение характеристики.

Для получения интервальных оценок необходимо знать закон распределения случайной величины.

Если показатель надежности подчиняется экспоненциальному закону распределения, то интервальную оценку этого показателя определяют из неравенства (2.10):

(2.10)

где 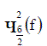и - квантили распределения, соответствующие вероятностям и и числу степеней свободы f = 2n, определяемые по таблице Б1 приложения Б.

Пример 3 Определим интервальную оценку математического ожидания из примера 1 при условии, что описываемая случайная величина подчиняется экспоненциальному закону.

Принимаем значение доверительной вероятности γ = 0,95, тогда

α = 1- γ = 0,05.

Тогда число степеней свободы f=2·15=30.

Этим значениям соответствуют квантили =46,97924 и

=16,79077, принятые по таблице Б1 приложения Б.

Так как значение математического ожидания известно, то для упрощения расчетов приведем формулу (2.10) к виду:

Таким образом, если случайная величина подчиняется экспоненциальному закону, то математическое ожидание времени исправного состояния рулевого управления автобуса «Autosan» находится в интервале 25,3 - 70,9 тыс. км.

Если показатель надежности подчиняется нормальному закону распределения, то интервальную оценку этого показателя определяют из неравенства:

(2.11)

где X и S – оценки математического ожидания и дисперсии; t ;f - квантиль распределения Стьюдента, соответствующая доверительной вероятности γ = 1 – α и числу степеней свободы f = n-1, определяемые по таблице Б2 приложения Б.

Пример 4 Определим интервальную оценку математического ожидания из примера 1 при условии, что описываемая случайная величина подчиняется нормальному закону.

При значении доверительной вероятности γ=0,95 и f=15-1=14 определим квантиль распределения Стьюдента по таблице Б2 приложения Б,

Если случайная величина подчиняется нормальному закону, то математическое ожидание времени исправного состояния рулевого управления автобуса «Autosan» находится в интервале 32,9 - 46,5 тыс. км.

Дата добавления: 2015-10-16