Проверка с помощью критерия Колмогорова

Критерий, предложенный А.Н. Колмогоровым, позволяет с достаточно большой достоверностью проверить, принадлежат ли статистические данные распределений вероятностей безотказной работы изделия к предполагаемому типу семейств законов распределения. Достоинством критерия Колмогорова является то, что его можно использовать для малых n (порядка единиц и десятков).

При проверке вычисляют значения эмпирической функции последовательно во всех интервалах и в этих же интервалах последовательно вычисляют значения теоретической функции. Затем находят интервал, в котором отклонение Dd, определяемое по формуле (5.8), принимает максимальное значение:

(5.7)

Далее проводят сравнение со значениями из таблицы Б6 приложения Б.

Гипотезу о характере закона распределения отвергают с вероятностью 1-α, если Dd > Dd, α, в противном случае эту гипотезу принимают.

Пример 9 С помощью критерия Колмогорова определим соответствие данных из примера 2 нормальному закону.

Определим значения интегральной функции распределения вероятностей на каждом интервале по теоретическому уравнению. Теоретическое уравнение для нормального закона имеет вид:

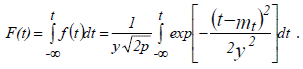(5.8)

Для облегчения вычислений интегралов используются специальные таблицы. Таблицы для нормального распределения в функции (t - mt) и σ были бы громоздкими, так как имели бы два параметра. Поэтому используют таблицы для нормального распределения, у которого mt = 0, σ = 1. Для этого распределения функция плотности имеет одну переменную Х:

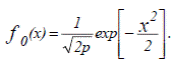(5.9)

Функция распределения будет иметь вид:

(5.10)

В литературе по надежности часто вместо интегральной функции распределения F0(x) используется функция Лапласса:

(5.11)

Очевидно, что

(5.12)

Эта функция протабулирована для различных значений x, и ее обычно представляют в виде таблицы (см. таблицу Б3 приложения Б).

При использовании таблицы следует применять подстановку

(5.13)

где х – квантиль нормированного нормального распределения.

Так как функция Лапласса нечетная, то справедливо равенство

(5.14)

Таблица 5.2 - Данные для вычисления критерия Колмогорова

Номер интервала j	Середина интервала xj	Теоретическое значение функции плотности распределения вероятности FT(xj)	Опытное значение функции плотности распределения вероятности FЭ (xj)	|FЭ - FT|
1	86,24	0,00	0,02	0,02
2	118,7	0,02	0,04	0,02
3	151,2	0,06	0,07	0,01
4	183,7	0,18	0,27	0,09
5	216,2	0,39	0,47	0,08
6	248,7	0,63	0,69	0,06
7	281,2	0,83	0,93	0,1
8	313,7	0,94	1,00	0,06
	max = 0,09

Далее проводим сравнение со значениями из таблицы Б6 приложения Б.

Гипотезу о характере закона распределения отвергают с вероятностью 1-α, так как Dd > Dd, α.

Дата добавления: 2015-10-16