Пример расчета №3

«Расчет переходного процесса в цепи, содержащей нелинейный резистор»

Схема цепи показана на рис. 5.48.

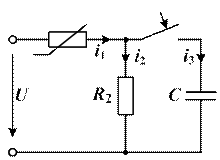
	Данные для расчета: В, Ом, Ом, мкФ. Вольт-амперная характеристика представлена на рис.5.39. Ток на вольт-амперной характеристике соответствует току на схеме.
Рис. 5.48

1. – момент коммутации.

2. Для по законам Кирхгофа составим систему уравнений:

, (5.24)

где u – напряжение на нелинейном резисторе.

Преобразуем данную систему к одному дифференциальному уравнению, в котором фигурируют только те переменные, которые описывают характеристику нелинейного элемента – для данной задачи напряжение на нелинейном резисторе u и ток через него .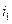

Из третьего уравнения системы (5.24) выражаем ток :

.

Выразив из второго уравнения системы (5.24) напряжение конденсатора , определяем ток через конденсатор:

.

Подставляя полученные выражения для токов и в первое уравнение системы (5.24), получим требуемое дифференциальное уравнение:

или, умножая на :

.

Подставляя численные значения параметров, получим расчетное уравнение

. (5.25)

Дифференциальное уравнение (5.25) является нелинейным, так как нелинейной является зависимость .

3. Определим рабочий участок на вольт=амперной характеристике.

3.1. Рассмотрим установившийся режим до коммутации ().

Так как в этом режиме конденсатор был не подключен к источнику энергии, напряжение на конденсаторе будет равно нулю:

В.

В соответствии с законом коммутации , тогда из второго уравнения системы (5.24) В. По вольт-амперной характеристике находим ток А. Таким образом, мы нашли координаты начала рабочего участка – точки А (рис.5.49).

3.2. Найдем напряжение на резисторе в установившемся режиме после коммутации ().

Поскольку в этом режиме в цепи действует источник постоянного напряжения, в уравнении (5.25) следует положить , в результате это уравнение приобретает вид:

. (5.26)

Тогда напряжение на нелинейном сопротивлении можно найти, как точку пересечения вольт-амперной характеристики с прямой (5.26). Найденная точка с координатами В, А определяет конец рабочего участка – точку В на рис.5.49.

Дата добавления: 2015-10-16