Метод кусочно-линейной аппроксимации

Аппроксимируем зависимость на участке АВ двумя отрезками прямых АС и СВ. Для этого выбираем положение точки С так, чтобы аппроксимация не слишком отличалась от реальной зависимости. Например, 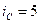А, 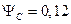Вб (рис.5.41).

1). Рассмотрим участок АС.

На этом участке отрезок аппроксимирующей прямой описывается следующим уравнением

, (5.4)

где 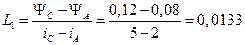Гн – эквивалентная индуктивность участка АС.

Это уравнение подставляем в уравнение (5.3) и получаем линейное дифференциальное уравнение относительно тока через индуктивность :

,

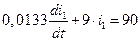откуда

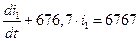. (5.5)

Решение уравнения (5.5) ищем в виде:

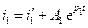, (5.6)

где 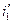– величина, соответствующая установившемуся режиму после коммутации (), 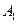– постоянная, определяемая начальными условиями, 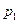– корень характеристического уравнения.

Характеристическое уравнение

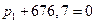
откуда 1/с.

Для установившегося режима после коммутации имеем 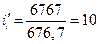А (при правильном выполнении преобразований должно равняться току точки В на рис.5.41).

Запишем (5.6) для момента коммутации ():

, откуда .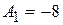

Окончательно решение уравнения (5.5) имеет вид:

А. (5.7)

Это решение действует на участке АС, которому соответствует интервал времени от до момента времени , соответствующего точке С. Найдем этот момент времени, используя выражение (5.7), записанное для точки С:

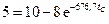, откуда 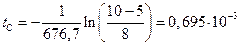с.

2). Рассмотрим участок СВ.

На этом участкеотрезок прямой описывается уравнением

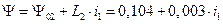, (5.8)

где 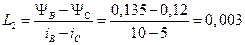Гн – эквивалентная индуктивность участка СВ.

Уравнение (5.8) подставляем в (5.3) и получаем линейное дифференциальное уравнение относительно тока через индуктивность 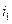для участка СВ:

. (5.9)

Поскольку это уравнение справедливо для участка СВ, на который мы попадаем спустя время 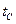после начала переходного процесса, решение ищем в виде:

. (5.10)

Характеристическое уравнение

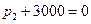
откуда 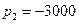1/с.

Для установившегося режима после коммутации имеем .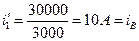

Запишем (5.9) для момент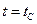а :

, откуда .

В результате решение уравнения (5.9) примет вид:

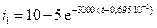А. (5.11)

На рис.5.42 построена зависимость изменения тока 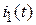по выражениям (5.7) и (5.11).

---

Дата добавления: 2015-10-16