Пример расчета

Схема рассчитываемой цепи приведена на рис. 3.2.

Начальные данные:

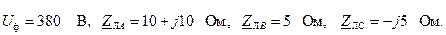
Параметры нагрузки, соединенной по схеме «звезда»:

Параметры нагрузки, соединенной по схеме «треугольник»:

Рис. 3.2

1. Рассчитаем полные сопротивления фаз нагрузки и линейных проводов.

1.1. Полные сопротивления линейных проводов:

.

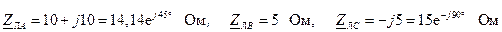1.2. Полные сопротивления фаз нагрузки («звезда»):

1.3. Полные сопротивления фаз нагрузки («треугольник»):

1.4. Преобразуем «звезду» в эквивалентный «треугольник»:

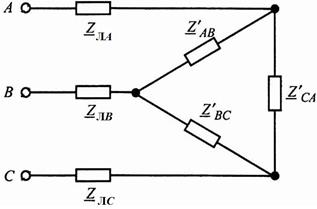
Первоначальная цепь (рис. 3.2) преобразуется в цепь, приведенную на рис. 3.3.

Рис. 3.3	Рис. 3.4

1.5. Данную цепь преобразуем в эквивалентный «треугольник» (рис. 3.4):

1.6. Преобразуем «треугольник в эквивалентную «звезду»» (рис. 3.5):

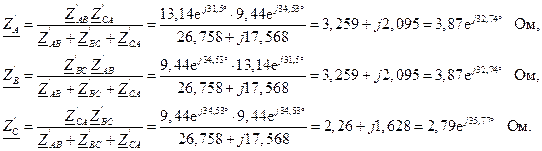
Рис. 3.5	Рис. 3.6

1.7. Полученную цепь преобразуем в упрощенную «звезду» (рис. 3.6).

Полные сопротивления фаз цепи, показанной на рис. 3.6:

Соответствующие полные проводимости:

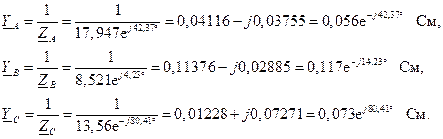
1.8. Рассчитаем упрощенную цепь по схеме «звезда».

Нагрузка фаз несимметрична, поэтому найдем напряжение смещения нейтрали:

.

Так как генератор симметричен, фазные ЭДС равны:

Рассчитаем падения напряжения в линейных проводах

Тогда токи в линейных проводах равны

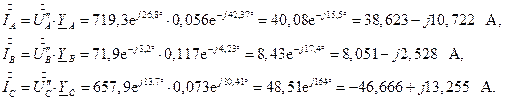
1.9. Рассчитаем падения напряжений на линейных проводах:

1.10. Фазные напряжения в «звезде» :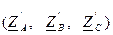

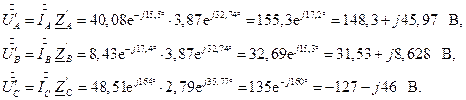
1.11. Используя второй закон Кирхгофа, рассчитаем линейные напряжения в «треугольнике» первоначальной цепи:

1.12. Рассчитаем токи в фазах «треугольника»:

1.13. Рассчитаем токи в линейных проводах, присоединенных к «треугольнику»:

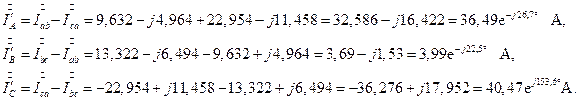
1.14. Рассчитаем фазные напряжения в первоначальной «звезде»:

1.15. Рассчитаем фазные токи в первоначальной «звезде»:

1.16. Рассчитаем напряжения смещения нейтрали первоначальной «звезды»:

2. Определим показания амперметров, используя результаты п.1.13.

3. Рассчитаем мощности нагрузок.

3.1 Нагрузка «звезда»:

3.2. Нагрузка «треугольник»:

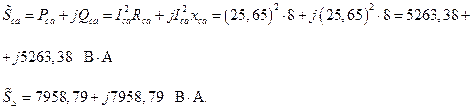
3.3 Мощность в линейных проводах:

3.4 Полная мощность нагрузок:

3.5. Рассчитаем мощности источников:

3.6. Проверим выполнение баланса мощности:

4. Определим показания ваттметров

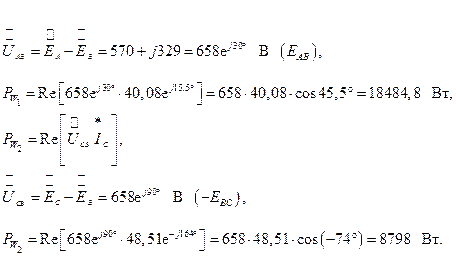
5. Построим топографическую диаграмму напряжений и токов на комплексной плоскости (рис. 3.7).

Рис. 3.7

ЗАДАНИЕ № 4

Дата добавления: 2015-10-16