Расчет токов во всех ветвях цепи методом узловых напряжений.

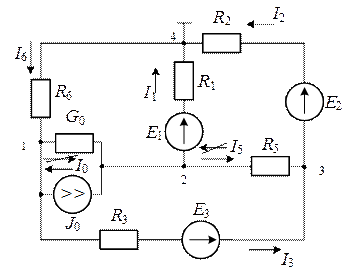
На рис. 1.49 изображена схема, по которой производим расчет. Она получается из первоначальной исключением ветви, содержащей R ₄ и Е ₄, (ток в этой ветви равен нулю, т.к. для него нет замкнутого пути), и ветвей, содержащих вольтметры (внутреннее сопротивление вольтметра →∞).

Рис. 1.49

Произвольно зададимся положительными направления токов в ветвях (они совпадают с ориентацией ветвей графа, показанного на рис. 1.42) и покажем их стрелками. Если в результате расчета токи получатся отрицательными, выбранные положительные направления этих токов нужно поменять (зачеркнуть) на противоположное (показать новой стрелкой).

Цифрами 1, 2, 3, 4 на схеме (рис. 1.49) пронумеруем узлы. За базисный узел примем узел 4 и будем считать его потенциал равным нулю ().

Найдем потенциалы остальных узлов.

Потенциалы узлов можно найти с помощью матричного уравнения

A G^(B)A^Tj= AJ^(B)-AG^(B) E^(B),

а напряжения ветвей по уравнению

U^(В) =A^Tj.

Рис. 1.50

Верхний индекс (В) означает принадлежность к ветви цепи, Т – знак транспонирования матрицы, G^(B) – диагональнаяматрица проводимостей ветвей, j – матрица-столбец потенциалов узлов, J^(B) – матрица-столбец токов источников тока, E^(B) – матрица-столбец ЭДС ветвей, U^(В) –матрица напряжений ветвей.

Если цепь простая (количество узлов мало), как в данном случае, узловые уравнения составляются непосредственно по схеме без использования матриц.

После расчета получим:

j₁ = –110,3 В, j₂ = –74,4 В, j₃ = –89,5 В.

По закону Ома для участка цепи, содержащего или не содержащего источник ЭДС, составим уравнения для нахождения токов во всех ветвях цепи

Подставим в эти формулы численные значения и рассчитаем токи

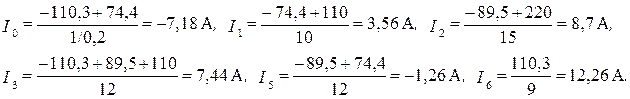
Токи I ₀ и I ₅ получились отрицательные, следовательно, их первоначально выбранное направление нужно поменять на противоположное.

Проверка токов производится по первому закону Кирхгофа.

Дата добавления: 2015-10-16