Операторный метод

Рассчитаем начальные условия для переменных:

, .

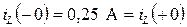Эти величины используются при написании уравнений цепи в операторной форме. Согласно законам Кирхгофа запишем следующую систему уравнений в операторной форме:

Подставим численные значения в данную систему

Приведем систему к операторному уравнению относительно операторного тока и сравним с ранее полученным решением

,

где A(p) – полином числителя и B(p) – полином знаменателя.

Рекомендуется проверить правильность полученного уравнения с помощью пределов:

.

Рассчитанные токи и совпадают с соответствующими токами, полученными по классическому методу.

Чтобы рассчитать ток будем использовать теорему разложения:

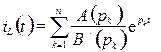_. (4.10)

1. Найдем корни из уравнения B(p)= 0

.

, , .

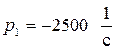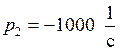2. Произведем дифференцирование

.

3. Рассчитаем коэффициент для корня :

4. Рассчитаем коэффициент для корня :

5. Рассчитаем коэффициент для корня :

6. Используя (4.10), получаем формулу для тока:

A.

Эта формула совпадает с выражением (4.9) для , полученным классическим методом. Токи в других ветвях и напряжение на реактивных элементах получают по аналогии.

ЗАДАНИЕ №5

Дата добавления: 2015-10-16