Пример расчета №2

«Расчет переходного процесса в цепи, содержащей нелинейный конденсатор»

Схема цепи показана на рис. 5.44.

	Данные для расчета: В, Ом, Ом, Ом. Кулон-вольтная характеристика представлена на рис.5.38.
Рис. 5.44

1. – момент коммутации.

2. Для составим систему уравнений, используя законы Кирхгофа:

. (5.13)

При этом ток через нелинейный конденсатор определяется выражением

.

Преобразуем данную систему к одному дифференциальному уравнению, в котором фигурируют только те переменные, которые описывают характеристику нелинейного элемента – для данной задачи заряд конденсатора q и напряжение на конденсаторе 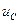. Для того, чтобы исключить переменные 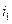и из системы (5.13), достаточно выразить их из второго и третьего уравнений и далее подставить соответствующие выражения в первое уравнение системы. В итоге получим требуемое дифференциальное уравнение:

.

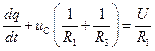Подставляя численные значения параметров, получим расчетное уравнение

. (5.14)

Дифференциальное уравнение (5.14) является нелинейным, так как нелинейной является зависимость .

3. Определим рабочий участок на кулон-вольтной характеристике.

3.1. Рассмотрим установившийся режим до коммутации ().

Так как постоянный ток через конденсатор не протекает, напряжение на конденсаторе будет равно приложенному:

В

и далее по вебер-амперной характеристике находим Кл.

Таким образом, мы нашли координаты начала рабочего участка – точки А (рис. 5.45).

3.2. Найдем напряжение на конденсаторе в установившемся режиме после коммутации ().

Поскольку в этом режиме в цепи действует источник постоянного напряжения, в уравнении (5.14) следует положить , тогда В. Найденное напряжение определяет конец рабочего участка – точку В на рис.5.45.

Дата добавления: 2015-10-16