|
Читайте также: |
165. Игральную кость бросили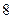 
раз. При этом 
очко выпало раз, 
очка – раз, 
очка – раз, 
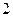очка – 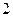раза, 
очков – 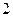раза, 
очков – раз. Найдите эмпирическую функцию распределения числа очков, выпавших при бросании игральной кости.
| Xi | 1 | 2 | 3 | 4 | 5 | 6 |
| Ni | 1 | 1 | 1 | 2 | 2 | 1 |
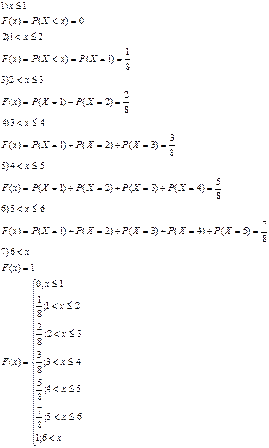
166. В четырех независимых испытаниях случайная величина 
приняла следующие значения: 
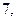
Найдите несмещенную оценку дисперсии 
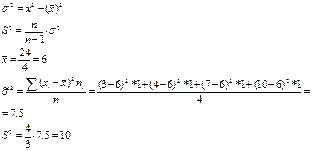
167. В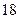 
независимых испытаниях случайная величина значениe приняла 
раз, а значение – 
раз. Найдите несмещенную оценку дисперсии
168. Даны результаты 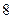независимых измерений одной и той же величины прибором, не имеющим систематических ошибок: 
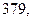
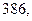
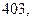
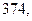
м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина 
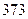м.
169. Даны результаты 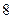независимых измерений одной и той же величины прибором, не имеющим систематических ошибок: 
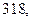
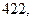
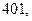
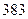м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина неизвестна.
170. Используя метод моментов, оцените параметры 
и 
равномерного распределения на отрезке 
по эмпирическому распределению
| Значение
| 3 | 5 | 7 | 9 |
| Частота | 21 | 18 | 15 | 26 |
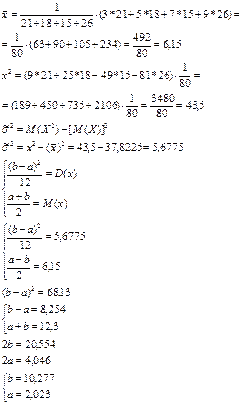
171. Случайная величина (время бесперебойной работы устройства) имеет показательное распределение с плотностью 
(
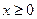). По эмпирическому распределению времени работы
| Время работы | 
| 
| 
| 
|
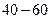
| Число устройств |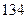 
| 
| 
|
|
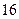
методом моментов найдите точечную оценку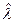 
.
172. Случайная величина распределена по закону Пуассона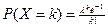 
. Результаты 
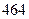независимых наблюдений отражены в таблице
| Значение
| 0 | 1 | 2 | 3 |
| Частота | 
| 
| 
| 
|
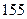
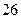
Найдите методом моментов точечную оценку .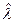
Дата добавления: 2015-10-16; просмотров: 48 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Двумерные непрерывные случайные векторы | | | Интервальные оценки параметров распределения |