Читайте также:
|
115. Для нормальной случайной величины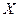 
с математическим ожиданием 
и дисперсией 
найдите вероятность 
.
116. Случайная величина 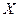имеет нормальное распределение с параметрами 
и 
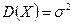. Найдите вероятность попадания 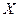в интервал 
.
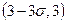117. Для нормальной случайной величины 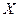известно, что математическое ожидание 
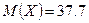и вероятность 
Найдите дисперсию 
.
118. Для нормальной случайной величины 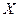известно, что дисперсия 
и вероятность 
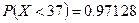. Найдите математическое ожидание 
.
119. Для нормальной случайной величины 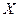с математическим ожиданием 
и дисперсией 
найдите вероятность 
.
120. Математические ожидания и дисперсии независимых нормальных случайных величин 
равны 1. Найдите вероятность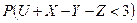 
.
121. Для нормальной случайной величины 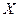с математическим ожиданием 
и дисперсией 
найдите вероятность 
.
122. Для независимых нормальных случайных величин ,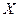 
известны их математические ожидания и дисперсии: 
, 
, 
, 
. Найдите вероятность 
.
123. Независимые нормальные случайные величины 
имеют одинаковые параметры: 
, 
, 
. Для случайной величины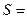 
найдите вероятность 
.
124. Для нормальной случайной величины 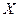с математическим ожиданием 
и дисперсией 
найдите вероятность 
.
125. Случайные величины 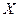и независимые и распределены по нормальному закону, причём 
, 
. Найдите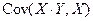 
.
Дата добавления: 2015-10-16; просмотров: 85 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Равномерное распределение на отрезке | | | Двумерные дискретные случайные векторы |