
Читайте также:
|
82. Даны математические ожидания случайных величин 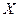 и
и  :
: 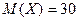 ,
,  , их дисперсии
, их дисперсии  ,
, 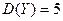 и ковариация Cov
и ковариация Cov 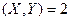 . Найдите математическое ожидание
. Найдите математическое ожидание 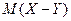 и дисперсию
и дисперсию 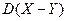 .
.

83. Случайные величины 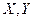 принимают только значения
принимают только значения 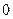 и
и 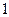 . Найдите дисперсию
. Найдите дисперсию 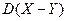 , если вероятности
, если вероятности 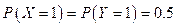 , а коэффициент корреляции
, а коэффициент корреляции 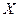 и
и  равен
равен 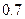 .
.
| X | 1 | 0 | Y | 1 | 0 |
| P | 0.5 | 0.5 | P | 0.5 | 0.5 |
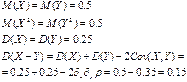
84. Для случайных величин 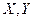 даны их математические ожидания и дисперсии
даны их математические ожидания и дисперсии  ,
, 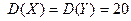 , а также коэффициент корреляции
, а также коэффициент корреляции 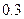 . Найдите математическое ожидание
. Найдите математическое ожидание  .
.
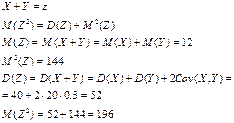
85. Случайные величины 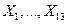 распределены по закону Пуассона с одинаковым математическим ожиданием, равным
распределены по закону Пуассона с одинаковым математическим ожиданием, равным 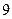 . Найдите математическое ожидание
. Найдите математическое ожидание 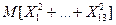 .
.
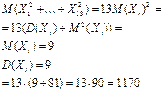
86. Случайные величины 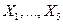 независимы и распределены по закону Пуассона с одинаковым математическим ожиданием, равным
независимы и распределены по закону Пуассона с одинаковым математическим ожиданием, равным 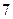 . Найдите математическое ожидание
. Найдите математическое ожидание 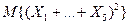 .
.
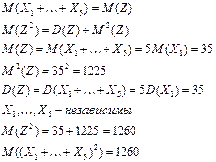
87. Случайные величины 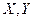 распределены по закону Пуассона. Найдите
распределены по закону Пуассона. Найдите  , если
, если 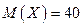 и
и 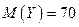 , а коэффициент корреляции
, а коэффициент корреляции 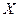 и
и  равен
равен  .
.
Дата добавления: 2015-10-16; просмотров: 90 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные дискретные законы распределения и их характеристики | | | Функция распределения и функция плотности непрерывной случайной величины |