Правила сложения и умножения вероятностей

17. Пусть – вероятности событий. Найдите наименьшую возможную вероятность события .

18. Вероятность события , , Найдите наименьшую возможную вероятность события .

19. В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего элементов соответственно равны , и . Найдите вероятность того, что тока в цепи не будет.

А-событие, сост. в том, что тока нет

-событие, сост. в том, что ток есть

=В1,В2,В3

Вi-событие, сост. в том, что прибор исправен

20. Вероятность хотя бы одного попадания в мишень при 9 выстрелах равна 0.81. Найдите вероятность попадания при одном выстреле.

А-событие, сост. в том, что при 9 выстрелах в мишень попадут 1 раз

P(A)=0.81

А с чертой – событие, сост. в том, что в мишень не попали ни разу

Вероятность непопадания при 1 выстреле

След, вероятность попадания 1 выстрела

21. Пассажир подходит к остановке автобусов двух маршрутов. Интервал движения автобусов 1-го маршрута составляет 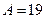мин., а 2-го маршрута – мин. Найдите вероятность того, что пассажир уедет с остановки не позднее, чем через мин., считая, что его устроит автобус как 1-го, так и 2-го маршрутов.

А-событие, сост. В том, что уедет не позднее, чем через 6 мин

-опоздает

В-1 авт. Прибудет позднее 6 мин

С – 2 авт. Прибудет позднее 6 мин

22. В ящике 8 белых и 13 черных шаров. Два игрока поочередно извлекают по шару, каждый раз возвращая его обратно. Выигрывает тот, кто первым вытащит белый шар. Какова вероятность выигрыша для начинающего игру?

А-событие, сост. в том, что достали белый шар

23. Вероятность того, что при одном измерении некоторой физической величины допущена ошибка, равна 0.05. Найдите наименьшее число измерений, которые необходимо произвести, чтобы с вероятностью можно было ожидать, что хотя бы один результат измерений окажется неверным.

А-хотя бы 1 раз результат окажется неверным

А с чертой- все верны

А с чертой= В1, …Вn

Bi- где i результат верен

Дата добавления: 2015-10-16