
|
Читайте также: |
45. Независимые дискретные случайные величины  принимают только целые значения:
принимают только целые значения: 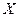 – от
– от  до
до  с вероятностью
с вероятностью  ,
,  – от
– от  до
до  с вероятностью
с вероятностью  . Найдите вероятность
. Найдите вероятность  .
.

46. Независимые случайные величины  принимают только целые значения:
принимают только целые значения: 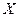 – от
– от  до
до  с вероятностью
с вероятностью 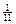 ,
,  – от
– от  до
до 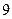 с вероятностью
с вероятностью  . Найдите вероятность
. Найдите вероятность  .
.

47. Независимые случайные величины  принимают только целые значения:
принимают только целые значения: 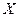 – от
– от  до
до  с вероятностью
с вероятностью  ,
,  – от
– от  до
до  с вероятностью
с вероятностью  . Найдите вероятность
. Найдите вероятность  .
.

48. Независимые случайные величины  принимают только целые значения:
принимают только целые значения: 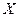 – от
– от  до
до  с вероятностью
с вероятностью  ,
,  – от
– от  до
до 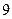 с вероятностью
с вероятностью  . Найдите вероятность
. Найдите вероятность  .
.

49. Независимые случайные величины 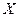 и
и  принимают только целые значения:
принимают только целые значения: 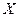 – от
– от  до
до 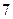 ,
,  – от
– от  до
до  . Найдите
. Найдите 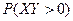 , если известно, что возможные значения
, если известно, что возможные значения 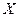 и
и  равновероятны.
равновероятны.

50. Независимые случайные величины  принимают только целые значения:
принимают только целые значения: 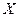 – от
– от  до
до 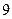 с вероятностью
с вероятностью  ,
,  – от
– от 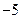 до
до  с вероятностью
с вероятностью  . Найдите
. Найдите  .
.

51. Независимые случайные величины  принимают только целые значения от
принимают только целые значения от 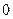 до
до  . Найдите вероятность
. Найдите вероятность  , если известно, что все возможные значения равновероятны.
, если известно, что все возможные значения равновероятны.

52. Независимые случайные величины 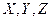 принимают только целые значения:
принимают только целые значения: 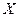 – от
– от  до
до  с вероятностью
с вероятностью  ,
,  – от
– от  до
до  с вероятностью
с вероятностью  ,
,  – от
– от  до
до 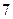 с вероятностью
с вероятностью 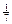 . Найдите вероятность того, что
. Найдите вероятность того, что 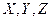 примут разные значения.
примут разные значения.

53. Независимые случайные величины 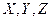 принимают только целые значения:
принимают только целые значения: 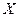 – от
– от  до
до  с вероятностью
с вероятностью  ,
,  – от
– от  до
до 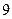 с вероятностью
с вероятностью  ,
,  – от
– от  до
до 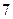 с вероятностью
с вероятностью 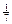 . Найдите вероятность
. Найдите вероятность  .
.

Дата добавления: 2015-10-16; просмотров: 94 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Схема Бернулли. Приближенные формулы Лапласа и Пуассона | | | Математическое ожидание и дисперсия дискретной случайной величины |