Тригонометрические ряды Фурье

Функция является одной из простейших периодических функций. Она описывает простейшее колебательное движение. Подобные функции называют гармоническими.

Рассмотри периодические функции, каждую из которых можно представить в виде суммы ряда: .

Мы научимся разлагать функцию в ряд такого типа.

Определение 5.1. Функции и 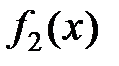называют попарно ортогональными на отрезке , если

.

Система функций называется ортогональной на отрезке , если любые две функции , , при ортогональны на .

Определение 5.2. Последовательность функций называют ортонормированной, если её элементы попарно ортогональны и .

Напомним определение кусочно-непрерывной функции.

Определение 5.3. Функцию, заданную на интервале , называют кусочно-непрерывной на этом интервале, если она непрерывна всюду на интервале 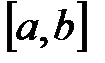, за исключением, быть может, конечного числа точек разрыва первого рода, причём в каждой точке разрыва , , эта функция удовлетворяет условию: , .

Теорема 5.4. Если 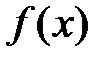– периодическая функция, – её период, то интегралы от по всякому отрезку длины равны между собою, то есть для любого :

.

Теорема 5.5. Тригонометрическая система функций

ортогональна на любом отрезке длиной .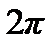

Доказательство.

Вычислим .

Мы знаем, что тогда ,

что и требовалось доказать.

Пример 1. В пространстве кусочно-непрерывных на интервале функций система функций

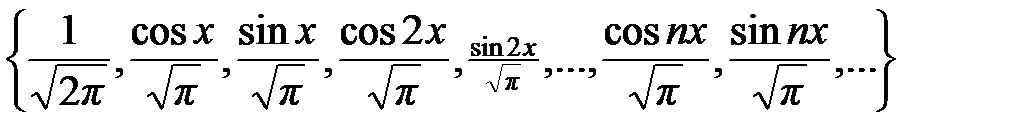
является ортонормированной.

Ортогональность данной системы функций доказана в теореме 1.6.

Вычислим , то есть система ортонормирована.

Для любой кусочно-непрерывной на интервале 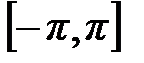функции тригонометрический ряд Фурье имеет вид:

,

где , , .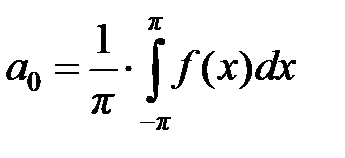

Достаточные условия разложимости функции в ряд Фурье дает теорема

Теорема 5.6. (Дирихле). Пусть функция – периодическая с периодом и кусочно-непрерывна (на каждом конечном интервале она и её производная имеют не более конечного числа точек разрыва первого рода) или кусочно-монотонна. Тогда в каждой точке непрерывности функция разложима в ряд Фурье, причем этот ряд сходится и в каждой точке разрыва функции к среднему арифметическому левого и правого пределов функции в точке . То есть , если – точка непрерывности функции; , если – точка разрыва функции.

Определение 5.7. Тригонометрическим рядом Фурье называют ряд по тригонометрической системе функций.

Дата добавления: 2015-10-16