Замечания.

1. Если 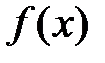– четная функция, то есть 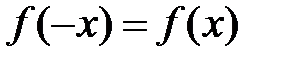, то , .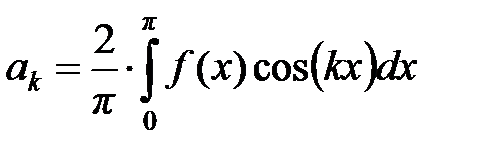

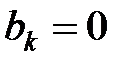
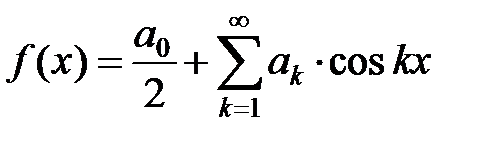2. Если 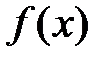– нечетная функция, то есть 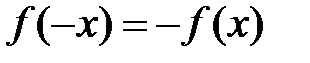, то , .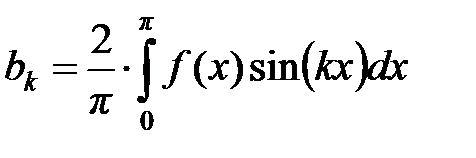

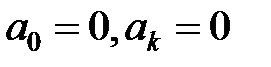
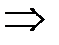
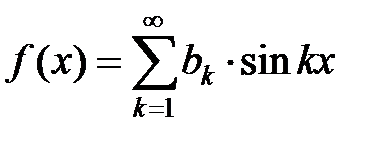Пример 2. Пусть функция 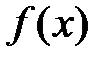периодична с периодом 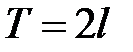и удовлетворяет условиям теоремы Дирихле. Тогда она разложима в ряд Фурье по ортогональной на отрезке 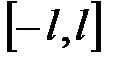системе функций 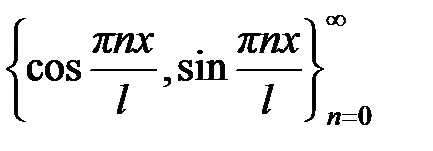. В каждой точке непрерывности функции 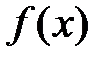разложение имеет вид:

,

,

.

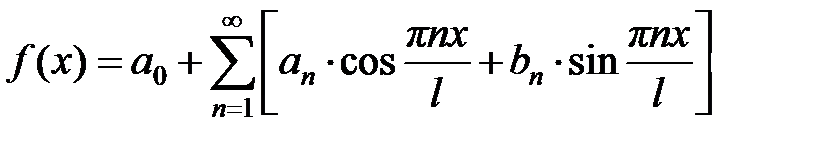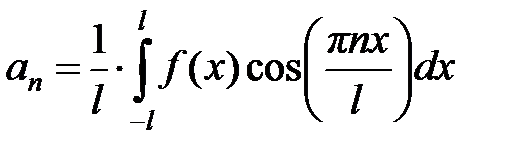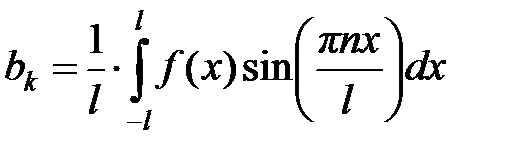В каждой точке разрыва 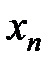ряд сходится к среднему арифметическому правого и левого пределов функции 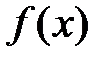в точке .

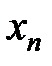Замечание. Функция, заданная на интервале 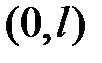, может быть разложена в ряд Фурье бесконечным числом способов в зависимости от того, как продолжить её на интервале 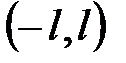; в частности, функцию 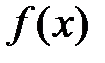, заданную на интервале 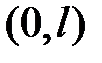, в зависимости от требований можно разложить либо в ряд только синусов, либо в ряд только косинусов. Тогда говорят: «Разложить функцию по синусам (или по косинусам)»

Пример 3. Разложить функцию 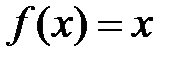в ряд. Указать интервалы, в которых сумма ряда 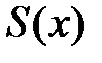совпадает с 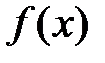, если 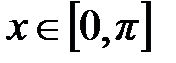. Найти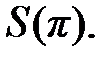

Решение. Заданная функция является непрерывной, но не является периодической. Чтобы были выполнены все условия теоремы Дирихле, функцию следует аналитически продолжить на всю ось по свойству периодичности. Из бесконечного числа возможных аналитических продолжений рассмотрим два частных способа продолжения функции:

a) По свойству нечетности. Тогда можно осуществить разложение функции в ряд по синусам;

b) По свойству четности. Тогда функцию разложим в ряд по косинусам.

Случай а) достраиваем функцию 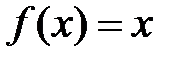на интервале 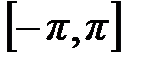как периодическую, нечетную. Её график симметричен относительно начала координат:

(РИС)

Вычислим коэффициенты 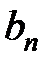ряда:

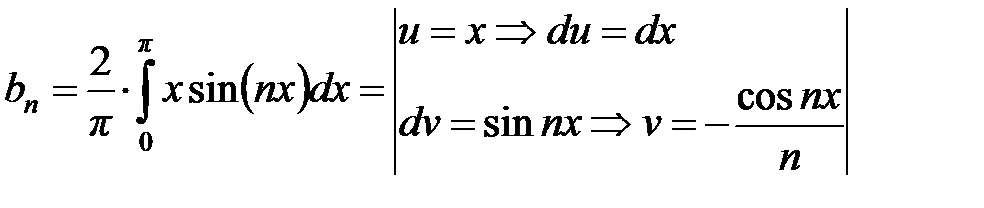
Учтём: 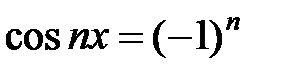, 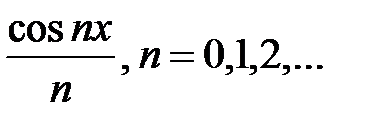. Поэтому 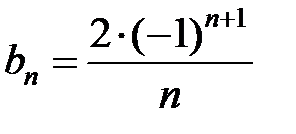. Зная коэффициенты 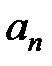и 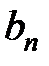составим ряд Фурье для функции :

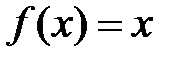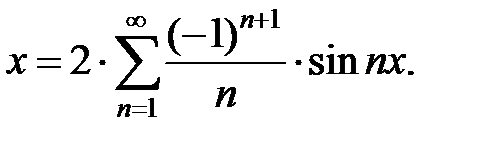
Построим 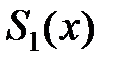. Сумма ряда во всех точках непрерывности функции совпадает с 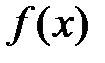, то есть 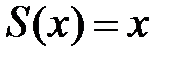. Точка 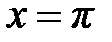является для функции точкой разрыва первого рода, поэтому то теореме Дирихле .

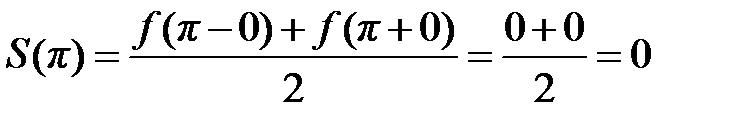Рассмотрим пункт b). Функцию 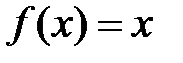на интервале 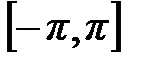достраиваем как периодическую, четную. Её график симметричен относительно начала координат:

(РИС)

В этом случае коэффициенты , .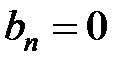

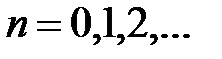Вычислим коэффициенты 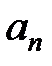ряда:

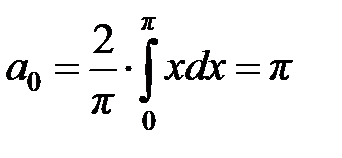
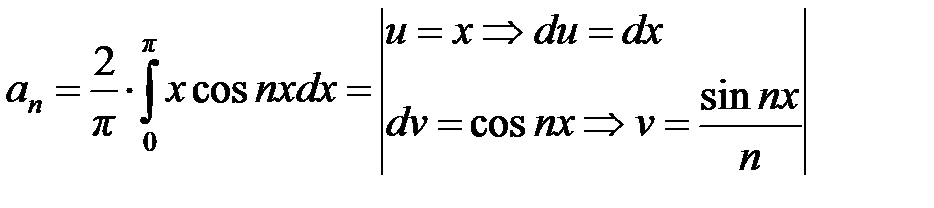
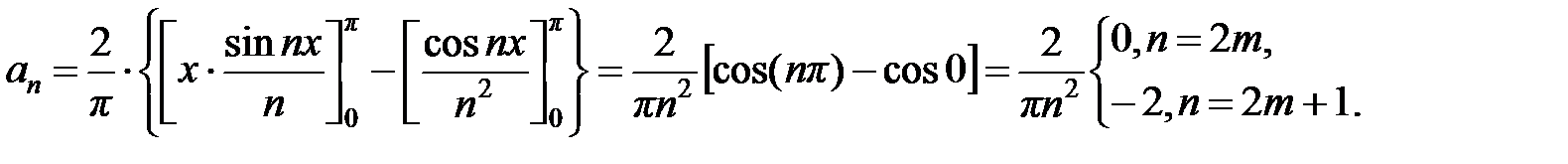
Запишем ряд Фурье для функции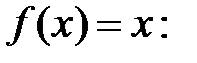

.

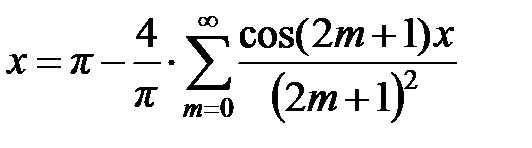Так как функция непрерывна для всех 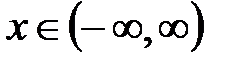, то .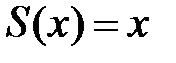

Сумма ряда во всех точках непрерывности функции совпадает с 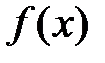, то есть .

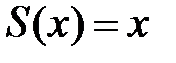Используя разложение 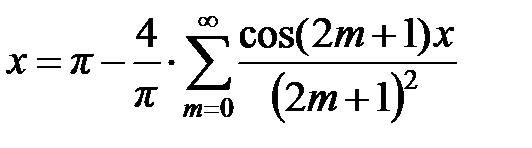для нахождения суммы числового ряда в точке 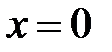имеем: 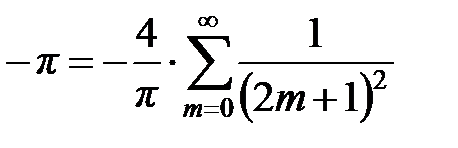, откуда находим сумму числового ряда: .

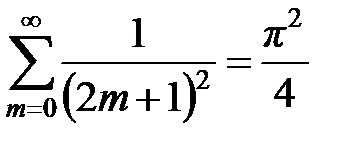Дата добавления: 2015-10-16