Интегральное преобразование Фурье.

На практике часто используются непериодические сигналы, поэтому обобщим ряд Фурье на случай непериодических сигналов и рассмотрим сигнал X_p(t), который представляет собой периодическую последовательность импульсов X(t), следующих с периодом T. X_p(t) = .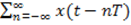

Функция X(t) описывает один импульс, коэффициенты ряда Фурье на интервале [-T/2;T/2] равны: Сk = * (3)

Учитывая, что сигнал на данном интервале может быть представлен одним импульсом, то за пределами указанного интервала X(t) = 0 и тогда (3) примет вид:

Сk = * (4)

Из (4) следует, что при T=const коэффициенты C_k зависят только от интервала и тогда:

X(k,w₁)= (5)

Комплексная функция частоты X(k,ω₁)– спектральная характеристика единичного импульса.

Из уравнения (4) и (5) можно записать следующее: C_k= (x(k,ω₁))/T;

Пределы интегрирования в уравнении (5) являются бесконечными, что следует понимать как разложение в ряд одноименного импульса на интервале [-∞;+∞] и тогда сигнал X(t) можно записать следующим образом, считая, что Tà∞:

X(t) = ;

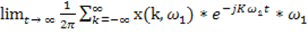Т.к. T = , то X(t) = (6)

Т.к. при Tà∞, частота первой гармоники ω₁ = , она становится бесконечно малой величиной. Приращение частоты ω₁ при переходе к соседней гармонике соответствует дифференциалу dω. Под знаком ∑ в (6) частотные гармоники принимают дискретные значения. Т.к. Tà∞, то частоты гармоник становятся бесконечно близкими.

Введём обозначение W = k*ω_1.

В этом случае в выражении (6) операция суммирования переходит в операцию интегрирования и тогда (5) и (6) имеют следующий вид:

X(ω) = 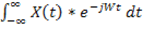(7)

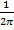X(t) = * (8)

Формулы (7) и (8) представляют собой непериодический сигнал X(t) на интервале

[-∞;+∞]. Соответственно в частотной и временной областях данной формулы называются

(7) – прямое и (8) – обратное преобразование Фурье.

Функции X(ω) характеризуют спектральный состав сигнала X(t) и называются спектральной плотностью сигнала X(t), т.е. если с помощью ряда Фурье можно разложить периодические сигналы на бесконечное число гармоник с частотами, принимающими дискретное значение, то интегральное преобразование Фурье позволяет получить непериодический сигнал в виде бесконечного числа гармоник, частоты которых бесконечно близки.

Дата добавления: 2015-10-21