Свойства интегрального преобразония Фурье.

Преобразование Фурье устанавливает взаимосвязь между предоставлением сигнала во временной и частотной областях.

Свойства:

1. Свойство вещественной и линейной частей спектральной плотности действительных

сигналов: вещественная часть X_R(ω) –является чётной функцией частоты, а

мнимая часть Xi(ω) –нечётной, а раз так, то X_R (ω) = X_R(-ω); XI (ω) = -X_I (ω);

2. Свойство линейности. Спектральная плотность комбинаций нескольких сигналов

будет определяться из уравнения: X(t) = a₁*x₁(t)+a₂*x₂(t);

В частотной области представляет такую же комбинацию линейных плотностей.

X(ω) = a₁*x₁(ω)+a₂*x₂(ω);

3. Свойство запаздывания: преобразование Фурье сигнала X(t), запаздывающего на τ₀

X(t –τ₀)=X(ω)* .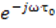

4. Свойство масштабирования: преобразование Фурье сигнала X(t), при изменении

масштаба времени в K-раз определяется следующим образом:

X(k,t) = (1/K)*X(ω/K).

5. Свойство спектральной плотности преобразования: это интегральное преобразование

Фурье, для которого производная сигнала X(t) определяется следующим

образом: X’(t) = ω*X(ω).

6. Спектральная плотность интегрального сигнала X(t) определяется: =x(ω)/jω;

7. Преобразование Фурье произведения сигналов определяется: X(t)*u(t)= *X(ω)*u(ω).

8. Преобразование Фурье свёртки сигналов во временной области:X(t)*U(t) =X(ω)*U(ω).

Дата добавления: 2015-10-21