Разложение периодических сигналов в ряд Фурье.

Элементы теории сигналов и систем.

Классификация сигналов по признакам.

Сигналы классифицируются по следующим признакам:

1) одномерные или многомерные (количество переменных больше 2х);

2) основанные на возможности или невозможности точного предсказания значения сигнала в любой момент времени или в любой точке пространственных координат. В 1-ом случае сигнал детерминированный, а во 2-м – случайный (описывается случайной функцией; cлучайную функцию времени называют случайным процессом)

V

V

Дискретизация сигнала заключается в замене непрерывных значений дискретными значениями и может осуществляться во времени, по уровню и во времени и уровню.

	t

а)детерминированная функция, (периодичная) б)случайная

Преобразование Фурье непрерывных сигналов.

Разложение периодических сигналов в ряд Фурье.

Сигнал x(t) называется периодическим, если x(t) = X(t+nT), где n = 1,2…; T-период сигнала;

Примером периодичного сигнала явл. гармонические колебания, кот. опис-ся следующим образом: x(t) = A*cos(ωt- φ); где A – амплитуда сигнала; ω – круговая частота; φ- начальная фаза сигнала; t – период; ω = 2πf; f = ; T = ;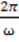

Сложение гармоник сигналов может быть представлено кратными частотами ω, 2 ω, образующих сигнал вида: x(t) = + +…;

Тогда, суммарный сигнал будет периодическим и будет определяться следующим уравнением: X(t) = (1)

где ω₁ – круговая частота 1-ой гармоники

В теории сигналов доказано, что периодический сигнал X(t) сложной формы может быть разложен на элементарные гармонические колебания с амплитудой А_к с частотой kω₁t и начальным сдвигом по фазе φ_k.

Разложим периодический сигнал:

A_k*cos(kω₁t – φ_k)=A_k*cos(kω₁t)*cos φ_k + A_k *sin(kω₁t)*sin φ_k;

Подставим A_k*cos φ_k = a_k; A_k sin φ_k = b_k;

Тогда, выражение (1) записанное с учётом нулевой гармоники, примет вид:

X(t) = + , (2)

где - нулевая гармоника;

Выражение (2) это разложение периодического сигнала в ряд Фурье.

Коэффициенты ряда Фурье определяются следующим образом:

a₀ = * ;

a_k = * ;

b_k = * ;

A_k =

Если x(t) – чётная функция на интервале [-T/2;T2], тогда

-> чётная функция, тогда коэффициент b_k ряда Фурье равен 0.

Если x(t) – нечетная, тогда 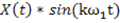-> не чётная функция, то все наоборот, и а_k = 0;

Совокупность А_к и φ_k разложенной периодической функции (1) представляют амплитудные и фазочастотные спектры вида: cosω₁t, sinω₁t, cos2ω₁t, sin2ω₁t, …, coskω₁t, sinkω₁t

Сумма функции, которая исп. в разложении (2), обладает свойством заключающемся в том, что интеграл произведений любых 2-х функций на периоде T равен нулю:

;

;

;

; p – действительное число, l – натуральное число.

Представление в полной записи называется ортогональностью, а разложение (2) X(t) по ортогональному базису функции выражения (1).

Дата добавления: 2015-10-21