Линейно-дискретный фильтр (ЛДФ)

Инвариантная к сдвигу схема - схема, для которой сдвиг входной последовательности на m-тактов приводит к сдвигу выходной последовательности: Y[n-m]=L{x[n-m]}, где L-операция преобразования ЛДС. Реакция ЛДС на единичный импульс называется импульсной характеристикой H[n].

Рассмотрим инвариантную к сдвигу ЛДС, преобразованную из базовых элементов:

x[n-1]A+x[n]=y[n-1]

В общем случае инвариантная к сдвигу ЛДС? построенная на основе базовых элементов функционирует на основе разностного уравнения, записанного в общем виде след. образом:

Y[n]= 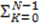B[k] x[n-k] - A[k]y[n-k] (20)

B[k] и A[k]-постоянные коэффициенты.

Цифровое устройство, реализующее (20) – это цифровой фильтр. Если известны коэффициенты отсчета входной послед-сти x[n], начальные знач-я ф-ии y[n-k], то, используя (20), можно вычислить Y[n] и для случая, когда n>=0, фильтр функции на основе (20) наз. рекурсивным.

Структурная схема рекурсивного фильтра:

; ;.. ; ;..

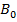Если в (20) a(k)=0, то фильтр будет нерекурсивным.

Характеристикой рассматриваемых фильтров(рек. и нерек.) явл-ся передаточная функция H(z)= Y(z) / X(z).

Выполнив z-преобразования над левой и правой частями (20), получим передаточную функцию рекурсивного фильтра:

Для нерекурсивного фильтра:

Существует несколько форм реализации рекурсивных фильтров:

1. Прямая (стр. схема рек.фильтра);

2. Каноническая (когда пределы в числителе и знаменателе одинаковые: N-1);

3. Последовательная

4. Параллельная

Дата добавления: 2015-10-21