
|
Читайте также: |
ЛАБОРАТОРНАЯ РАБОТА
Минск 2005
1. АНАЛОГОВЫЕ НИЗКОЧАСТОТНЫЕ ФИЛЬТРЫ-ПРОТОТИПЫ
Фильтр нижних частот представляет собой устройство, которое пропускает сигналы низких частот и задерживает сигналы высоких частот. В общем случае определим полосу пропускания как интервал частот 0< < с, полосу задерживания как частоты > с, переходную область как диапазон частот с < < 1 (с – частота среза). Эти частоты обозначены на рис. 1, на котором приведена реальная амплитудно-частотная характеристика фильтра нижних частот, где в данном случае заштрихованные области представляют собой допустимые отклонения характеристики в полосе пропускания и задерживания.

| 
|
| Рис. 1. Реальная амплитудно-частотная характеристика фильтра нижних частот. | Рис 2. Логарифмическая характеристика фильтра нижних частот. |
Если минимальное затухание выбрать за нормированный уровень 0 (А =1 на рис. 1), то логарифмическая характеристика фильтра нижних частот имеет вид, изображенный на рис. 2. Максимальное затухание в децибелах в полосе пропускания составляет 1, а минимальное затухание в полосе задерживания 2 (А 1 и А 2 – соответственно значения амплитудно-частотной характеристики). Затухание 1 не может превышать 3 дБ, в то время как типовое значение 2 значительно больше и может находиться в пределах 20 2100 дБ (в этом случае имеем 0,1 А 20,00001).
Коэффициент усиления фильтра нижних частот представляет собой значение его передаточной функции при s =0 или, что эквивалентно, значение его амплитудно-частотной характеристики на частоте =0. Следовательно, коэффициент усиления реального фильтра с амплитудно-частотной характеристикой, показанной на риc. 1, равен А.
Существует много типов фильтров нижних частот, удовлетворяющих данному набору технических требований, таких, как А 1, А 2, с, 1, обозначенных на рис. 1, или 1, 2, с, 1 – на рис. 2. Фильтры Баттерворта, Чебышева, инверсные Чебышева и эллиптические образуют четыре наиболее известных класса. Фильтр Баттерворта обладает монотонной характеристикой, подобной характеристике на рис. 1 и рис. 2. (Характеристика является монотонно спадающей, если она никогда не возрастает с увеличением частоты.) Характеристика фильтра Чебышева содержит пульсации (колебания передачи) в полосе пропускания и монотонна в полосе задерживания. На рис. 3 изображен вид характеристики фильтра Чебышева шестого порядка. Инверсная характеристика фильтра Чебышева монотонна в полосе пропускания и обладает пульсациями в полосе задерживания. Пример характеристики фильтра шестого порядка приведен на рис. 4.

| 
|
| Рис. 3. Амплитудно-частотная характеристика фильтра Чебышева шестого порядка. | Рис. 4. Амплитудно-частотная характеристика инверсного фильтра Чебышева шестого порядка. |
1.1. Фильтры Баттерворта
Вероятно, наиболее простая амплитудно-частотная характеристика фильтра нижних частот у фильтра Баттерворта, которая в случае n -го порядка определяется следующим образом:
 , (n= 1,2,3…). , (n= 1,2,3…).
| (1) |
Эта характеристика фильтра Баттерворта монотонно спадает (никогда не возрастает) при увеличении частоты. Увеличение порядка также приводит к улучшению характеристики.
Фильтр Баттерворта представляет собой полиномиальный фильтр и в общем случае обладает передаточной функцие й вида:

| (2) |
где К – постоянное число. Для нормированного фильтра, т. е. при с =1 рад/с, передаточную функцию можно записать в виде произведения сомножителей для n =2, 4, 6... как
 , ,
| (3) |
или для n =3, 5, 7,... как

| (4) |
Чем выше порядок фильтров, тем лучше их амплитудно-частотная характеристика. Однако более высокий порядок усложняет схемную реализацию и вследствие этого повышает стоимость. Таким образом, для разработчика представляет интерес выбор минимально необходимого порядка фильтра удовлетворяющего заданным требованиям.
Другими словами, предположим, что в изображенной на рис. 2 общей характеристике заданы максимально допустимое затухание в полосе пропускания 1 (дБ), минимально допустимое затухание в полосе задерживания 2 (дБ), частота среза с (рад/с) или fс (Гц) и максимальная допустимая ширина переходной области TW, которая определяется следующим образом
| TW = 1– 2. | (5) |
(Следовательно, полоса задерживания должна начинаться с некоторой частоты 2 1.) Задача состоит в нахождении минимального порядка n, который будет удовлетворять всем этим условиям.
Для фильтра Баттерворта минимальный порядок можно определить, подставив приведенные выше условия в (1) и решив его относительно порядка n. В результате получаем
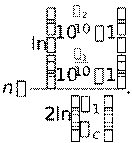
| (6) |
Уравнение (5) можно записать в виде
| 1/ с =(TW / c)+1, | (7) |
и полученное соотношение подставить в (6) для нахождения зависимости порядка n от ширины переходной области, а не от частоты 1. Параметр TW / c называется нормированной шириной переходной области и является безразмерной величиной. Следовательно, ТW и c можно задавать и в радианах на секунду, и в герцах.
Амплитудно-частотная характеристика фильтра Баттерворта наиболее плоская около частоты =0 по сравнению с характеристикой любого полиномиального фильтра n -го порядка и вследствие этого называется максимально плоской. Следовательно, для диапазона низких частот характеристика фильтра Баттерворта наилучшим образом аппроксимирует идеальную характеристику. Однако для частот, расположенных около точки среза и в полосе задерживания, характеристика фильтра Баттерворта заметно уступает характеристике Чебышева, который рассматривается ниже.
Однако фазочастотная характеристика фильтра Баттерворта лучше (более близка к линейной), чем соответствующие фазочастотные характеристики фильтров Чебышева, инверсных Чебышева и эллиптических сравнимого порядка. Это согласуется с общим правилом для фильтров данного типа – чем лучше амплитудно-частотная характеристика, тем хуже фазочастотная, и наоборот.
1.2. Фильтры Чебышева
Фильтр Чебышева обладает амплитудно-частотной характеристикой, которая определяется следующим образом:
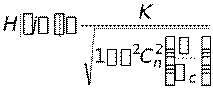 , (n =1, 2, 3...). , (n =1, 2, 3...).
| (8) |
Параметры и К – постоянные числа, а Сn является полиномом Чебышева первого рода степени n и имеет вид:
| Cn (x)=cos(n arcos(x)). | (9) |
Амплитудно-частотная характеристика достигает своего наибольшего значения К в тех точках, где Сn равно нулю. Поскольку эти точки распределены по полосе пропускания, то характеристика фильтра Чебышева содержит пульсации в полосе пропускания и монотонна в других областях. Размах этих пульсаций определяет параметр , а их число степень n. Коэффициент усиления фильтра определяется значением К.
Фильтр Чебышева иногда называют равноволновым фильтром, поскольку все пульсации равны по значению. Для К =1, т.е. на рис. 3 A=1, размах пульсаций RW = A A 1 для фильтра Чебышева будет равен
 . .
| (10) |
Таким образом, как угодно можно уменьшить RW, выбрав значение параметра достаточно малым.
Минимально допустимое затухание в полосе пропускания – постоянный размах пульсаций, часто выражается в децибелах как
 , ,
| (11) |
и может использоваться как характеристика фильтра Чебышева. Например, фильтр с неравномерностью передачи 1/2 дБ обладает таким значением , что =1/2 (это дает =0,3493). В общем случае, решая уравнение (11) относительно , можно получить
 . .
| (12) |
Наибольшим допустимым размахом пульсаций обладает фильтр Чебышева с неравномерностью передачи 3 дБ, для которого в (11) =1 (если говорить более точно, то необходимо иметь значение =0,99763, поскольку 1оg10(2) не равен точно 0,3).
По амплитудно-частотной характеристике на рис. 1 определяем А =1, а  . Для данного случая также можно точно определить А 2, которое установило бы значение частоты 1. Частота c=1 рад/с представляет собой точку среза или граничную точку полосы частот с пульсациями. Если интересуются значением частоты 3дБ,т. е. точкой, в которой характеристика спадает на 3 дБ, то получают:
. Для данного случая также можно точно определить А 2, которое установило бы значение частоты 1. Частота c=1 рад/с представляет собой точку среза или граничную точку полосы частот с пульсациями. Если интересуются значением частоты 3дБ,т. е. точкой, в которой характеристика спадает на 3 дБ, то получают:
 . .
| (13) |
Следует отметить, что c = 3 дБ если =1, и в этом случае получаем фильтр Чебышева с неравномерностью передачи 3 дБ.
На основе (8) для К =1 найдем минимальный порядок фильтра Чебышева:
 . .
| (14) |
Амплитудно-частотная характеристика фильтра Чебышева данного порядка лучше амплитудно-частотной характеристики Баттерворта, так как у фильтра Чебышева уже ширина переходной области. Однако фазочастотная характеристика фильтра Чебышева хуже (более нелинейна) по сравнению с фазочастотной характеристикой фильтра Баттерворта. Фазочастотные характеристики фильтра Чебышева для 2–7-го порядков приведены на рис. 5. Для сравнения на рис. 5 штриховой линией изображена фазочастотная характеристика фильтра Баттерворта шестого порядка. Можно также отметить, что фазочастотные характеристики фильтров Чебышева высокого порядка хуже фазочастотных характеристик фильтров более низкого порядка. Это согласуется с тем фактом, что амплитудно-частотная характеристика фильтра Чебышева высокого порядка лучше амплитудно-частотной характеристики фильтра более низкого порядка.

Рис. 5. Фазочастотные характеристики фильтров Баттерворта и Чебышева.
1.3. Эллиптические фильтры
Эллиптический фильтр имеет амплитудно-частотную характеристику, которая содержит пульсации как в полосе пропускания, так и в полосе задерживания и является лучшим среди всех фильтров нижних частот в том смысле, что для заданного порядка и допустимых отклонений характеристик в полосах пропускания и задерживания обладает самой узкой шириной переходной области. Пример амплитудно-частотной характеристики эллиптического фильтра пятого порядка изображен на рис. 6.

Рис. 6. Амплитудно-частотная характеристика эллиптического фильтра нижних частот для случая n =5.
Пульсации в полосе пропускания равны по значению и могут характеризоваться максимальным допустимым затуханием в полосе задерживания. Эта величина которую мы также будем называть неравномерностью передачи, в полосе пропускания (РRW), дБ, согласно обозначению на рис. 6 равна:
| PRW =–20log10(A 1). | (15) |
Пульсации в полосе пропускания так же равны по значению (хотя не обязательно равны размаху пульсаций в полосе пропускания) и характеризуются минимальным затуханием в полосе задерживания МSL, дБ, следующим образом:
| MSL =–20log10 (A 2). | (16) |
Ширина переходной области ТW, как и для других типов фильтров, составляет:
| TW = 1– c. | (17) |
Для заданных значений РRW и МSL повышение порядка приводит к увеличению числа пульсаций в полосах пропускания и задерживания и уменьшению TW. Следовательно, можно задать обозначенные на рис. 6 параметры А 1, A 2 и c и, увеличивая порядок, достичь любого требуемого значения 1> c.
В виде произведения сомножителей передаточная функция эллиптическая фильтра нижних частот четного порядка n записывается следующим образом:
 , ,
| (18) |
а нечетного порядка n
 , ,
| (19) |
где А 0, с 0, Аi, аi, bi, ci – заданные постоянные числа.
Постоянные параметры аi, bi и ci вычисляются крайне сложно. Этот процесс требует знания эллиптических функций Якоби.
2. ЦИФРОВЫЕ ФИЛЬТРЫ
2.1. Основы цифровой фильтрации
Цифровым фильтром называется цифровая система, используемая для фильтрации дискретных сигналов. Он может быть реализован или программным методом на ЭВМ, или с помощью специальной аппаратуры, и в каждом из этих случаев цифровой фильтр можно применить для фильтрации сигналов в реальном времени или для фильтрации предварительно записанных сигналов.
Аналоговый сигнал с ограниченным спектром можно преобразовать в дискретный посредством дискретизации. Полученный таким образом дискретный сигнал можно на основании теоремы отсчетов снова превратить в исходный аналоговый сигнал посредством интерполяции. Поэтому для решения задач фильтрации в реальном времени можно использовать цифровые фильтры, которые в недавнем прошлом решались с помощью аналоговых фильтров.
Преимущества, получаемые при этом, связаны с традиционными преимуществами цифровых систем вообще и заключаются в следующем:
1) некритичности к вариациям параметров компонентов;
2) нечувствительности к уходу параметров компонентов и внутренним помехам;
3) высокой точности;
4) малых физических размерах;
5) высокой надежности.
Очень важным дополнительным преимуществом цифровых фильтров является простота перестройки их параметров, что необходимо для изменения характеристик фильтров. Это свойство позволяет разрабатывать программируемые фильтры, решающие одновременно несколько задач фильтрации.
Цифровые сигналы вне зависимости от способа их получения представляются в виде последовательности чисел.
Во "временной" области цифровая система описывается набором разностных уравнений. Это значит, что при заданной входной последовательности и начальных условиях системы разностные уравнения единственным образом определяют выходную последовательность.
Наиболее подходящим методом решения линейных разностных уравнений является z -преобразование. Оно позволяет заменить решение этих уравнений решением алгебраических уравнений. Применение z -преобразования к разностным уравнениям аналогично применению преобразования Лапласа к дифференциальным уравнениям.
Основные проблемы цифровой фильтрации связаны с дискретизацией непрерывного сигнала, для получения его цифрового аналога. Эту теорему можно сформулировать следующим образом: непрерывную аналоговую функцию x (t), имеющую ограниченный спектр (т. е. спектр X (jw) такой, что X (jw)=0 при w > wm), можно однозначно описать, зная ее значения в моменты времени, равномерно распределенные и отстоящие друг от друга на интервал Т, где
| Т =2 / s и s 2 m. |
Важно отметить, что спектр дискретизированного сигнала получается путем периодического продолжения исходного ограниченного по частоте Зпектра с периодом, равным ws. При несоблюдении условий теоремы Котельникова мы получим явление, называемое наложением или эффектом отражения. В этом случае нельзя восстановить непрерывный исходный сигнал из соответствующей дискретизированной последовательности.
2.2. Реализация цифровых фильтров
2.2.1. Виды дискретных фильтров.
Линейный дискретный фильтр описывается линейным разностным уравнением:
 , ,
| (20) |
Значения выходной последовательности y (n) в момент n определяются N значениями входной последовательности и M –1 значениями самой выходной последовательности в “прошлые” моменты.
Фильтры, описываемые уравнением (20) называются рекурсивными.
В частном случае, при am =0, m =1, 2,..., из (31) получаем:
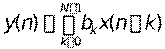 , ,
| (21) |
т. е. в этом случае значения выходной последовательности в любой момент определяется лишь значениями входной последовательности в этот же момент и N –1 “прошлыми” значениями входной последовательности. Фильтры, описываемые уравнением (21), называются нерекурсивными.
Алгоритмы рекурсивных и нерекурсивных фильтров могут быть представлены в виде структурных схем, в которых используются реализации трех операций – алгебраического сложения, умножения на константу и задержки на один интервал дискретизации.

Рис. 7. Структурная схема рекурсивного фильтра.

Рис. 8. Структурная схема нерекурсивного фильтра.
Фильтром с конечной импульсной характеристикой – КИХ-фильтром – называют фильтр, у которого импульсная характеристика представляет собой конечный дискретный сигнал (N -точечный дискретный сигнал), т.е. может принимать отличные от нуля значения лишь при n =0, 1,..., N –1.
Фильтром с бесконечной импульсной характеристикой – БИХ-фильтром – называют фильтр, у которого импульсная характеристика может принимать отличные от нуля значения на бесконечном множестве значений n =0, 1,...
Очевидно, что нерекурсивный фильтр всегда является КИХ-фильтром, в то же время рекурсивный фильтр может быть как БИХ-фильтром, так и КИХ-фильтром. Поскольку основные особенности проектирования и применения фильтров связаны с видом импульсной характеристики (КИХ или БИХ), а не с наличием или отсутствием обратной связи, будем, как правило, использовать термины “КИХ-фильтр” и “БИХ-фильтр”, а не “нерекурсивный” и “рекурсивный” фильтры [12].
2.3. Расчет цифровых БИХ- и КИХ-фильтров
Подобно аналоговым фильтрам расчет цифровых фильтров включает в себя процесс нахождения подходящей передаточной функции, которая должным образом удовлетворяет предъявленным требованиям. Характеристики цифровых фильтров часто задаются в частотной области. Частотная характеристика Н (е jq) цифрового фильтра является непрерывной функцией переменной q с периодом 2 p:
| Н (е j)= Н [е j ( + m2)], | (22) |
где m – целое число. Период обычно выбирается в пределах от - p до p. Это означает, что если Н (е jq) определена для q от - p до p, то она определена и для всех q. Записывая Н (е jq) в экспоненциальной форме, получаем
| Н (е j)= Н (е j)e– j (), | (23) |
где ï Н (е jq)ï называется амплитудно-частотной характеристикой, а j (q) – фазовым углом (запаздывания) фильтра.
Поскольку амплитудно-частотные характеристики представляют собой четные функции, а фазовые – нечетные, то достаточно определить частотную характеристику Н (е jq) цифрового фильтра для q в пределах от 0 до p вдоль верхней половины единичной окружности в z -плоскости.
При расчете фильтров удобнее использовать квадрат амплитудной функции и групповое время, чем амплитудно-частотную и фазовую характеристики. Квадрат амплитудной функции задается следующим соотношением:
| H (e j)2= H (z) H (z –1), при z =e j. | (24) |
Групповое время t (q) характеризует задержку отклика фильтра и определяется следующим образом:
| ()= d ()/ d. | (25) |
Наиболее желательная характеристика группового времени представляет собой приблизительно постоянную величину для частот в полосе пропускания фильтра.
В задачу проектирования фильтров входит нахождение частотной характеристики или передаточной функции, параметры которых удовлетворяют предъявленным к фильтру техническим требованиям. Следовательно, в своей основе расчет фильтра представляет собой процесс нахождения математической аппроксимации. Для математической аппроксимации используется набор базовых функций, которые позволяют систематизировать методику расчета. Решением задачи аппроксимации является одна или несколько функций, принадлежащих этому семейству базовых функций. Для цифровых фильтров реализуемые функции представляют собой и полиномы, и рациональные функции переменной z –1. Цифровой фильтр, который описывается передаточной функцией в виде полинома
| Н (z)= a 0+ a 1 z -1+...+ a M z –M, | (26) |
называется цифровым фильтром с конечной импульсной характеристикой (КИХ-фильтр). С другой стороны, цифровой фильтр, который задается передаточной функцией в виде рациональной функции
 , ,
| (27) |
называется цифровым фильтром с бесконечной импульсной характеристикой (БИХ-фильтр). Для КИХ-фильтров отсутствуют проблемы, связанные с их устойчивостью и физической реализуемостью, поскольку все КИХ-фильтры устойчивы и физически реализуемы. Цифровые БИХ-фильтры устойчивы, если все полюсы функции Н (z), заданной выражением (27), расположены внутри единичного круга в z -плоскости и физически реализуемы, если bk – первый ненулевой коэффициент знаменателя, а в числителе тогда коэффициенты равны a 0= a 1=...= ak -1=0. Вследствие того, что рассматриваются исключительно физически реализуемые фильтры, обычно полагают b 0=1. Следовательно, общая передаточная функция цифрового БИХ-фильтра задается в виде:
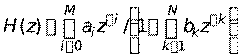 . .
| (28) |
2.3.1 Расчет цифровых БИХ-фильтров
Для цифровых БИХ-фильтров передаточные функции задаются соотношениями вида (29).
 . .
| (29) |
Заметим, что при замене переменной z на s выражение (29) представляет собой передаточную функцию аналогового фильтра. Сходство передаточных функций цифровых и аналоговых фильтров приводит к тому, что одним из наиболее целесообразных подходов к проектированию цифровых БИХ-фильтров является нахождение в некотором смысле цифровых вариантов методов расчета аналоговых фильтров. Реализация этого подхода требует разработки простых алгоритмов, которые обеспечивают переход от расчета аналоговых фильтров к расчету цифровых. Это означает, что расчет цифровых БИХ-фильтров состоит из следующих двух этапов.
Этап 1. Получение подходящей передаточной функции H (s), которая удовлетворяет требованиям задачи обработки сигнала.
Этап 2. Создание процедуры перехода, которая преобразует функцию H (s) в соответствующую передаточную функцию H (z), для получения метода расчета цифрового БИХ-фильтра, удовлетворяющего заданным техническим требованиям.
Такая методика наиболее целесообразна при проектировании фильтров с типовыми характеристиками, таких, как фильтры нижних и верхних частот, полосовые и заграждающие, для которых имеется хорошо разработанный аппарат аналоговой фильтрации.
1. Метод инвариантности импульсной характеристики.
Процедура перехода от аналоговых фильтров к цифровым фильтрам называется методом инвариантности импульсной характеристики. Эта процедура устанавливает, что импульсная характеристика h (n) результирующего цифрового фильтра представляет собой выборки импульсной характеристики h (t).
Этап 1. Задано: набор технических характеристик фильтра.
Этап 2. Найти передаточную функцию H (s) аналогового фильтра, удовлетворяющую заданным характеристикам.
Этап 3. Найти h (t) – импульсную характеристику аналогового фильтра, полученного на этапе 2.
Этап 4. Определить импульсную характеристику h (n) цифрового фильтра в виде h (n)= h (t) при t = nDt.
Этап 5. Найти передаточную функцию H (z) цифрового фильтра с помощью z -преобразования импульсной характеристики, полученной на этапе 4, следующим образом:
| . | (30) |
Этап 6. Результат: цифровой фильтр, полученный на этапе 5, удовлетворяющий требованиям этапа 1.
Однако метод инвариантности импульсной характеристики не является простым линейным отображением. Из-за эффекта наложения этот метод применим только для фильтров с существенно ограниченной аналоговой частотной характеристикой, т. е. в случаях фильтров нижних частот и полосовых.
2. Метод билинейного преобразования.
Эффект наложения в методе инвариантности импульсной характеристики вызывается тем, что отсутствует однозначная функция перехода из s- плоскости в z -плоскость. Для исключения этого нежелательного эффекта наложения необходимо определить однозначное непрерывное отображение. Одним из таких преобразований является билинейное преобразование, которое определяется следующим образом:
| . | (31) |
Графически билинейное преобразование выглядит так:

Данное преобразование отображает точку (0; 0) в точу (1; 0), а (0; ¥) и (0; -¥) — в точку (-1; 0).
Билинейное преобразование (31) – однозначная функция. Это означает, что каждой точке в z -плоскости соответствует только одна точка в s- плоскости и наоборот. Из этого свойства однозначности следует, что отсутствует эффект наложения спектров при билинейной процедуре отображения. Методика расчета цифровых фильтров на основе метода билинейного преобразования включает в себя нахождение подходящей передаточной функции Н (s) аналогового фильтра и применение к ней билинейного преобразования (31) для получения передаточной функции Н (z) требуемого цифрового фильтра.
При этом преобразовании будут сохраняться и частотные характеристики, и свойства устойчивости аналогового фильтра. Однако это не означает, что частотные характеристики аналогового и цифрового фильтров идентичны, одинакова только их “форма”. Например, если амплитудно-частотная характеристика аналогового фильтра монотонно спадает для 0< w <¥, то соответствующий цифровой фильтр, полученный с помощью соотношения (31), будет обладать монотонно спадающей амплитудно-частотной характеристикой от 0 до p. Однако соотношение между цифровой частотной переменной q и аналоговой частотной переменной w нелинейно:
| . | (32) |
Билинейное преобразование обеспечивает простую процедуру перехода от аналоговых к цифровым фильтрам и сохраняет вид частотных характеристик при преобразовании. Это означает, что широкополосные аналоговые фильтры с крутой переходной областью отображаются в широкополосные цифровые фильтры без эффекта наложения. В этом заключается основное преимущество этого метода по сравнению с методом инвариантности импульсной характеристики. Недостатком билинейного преобразования является то, что нелинейность соотношения между цифровой частотой и аналоговой частотой приводит к искажению частотных характеристик аналоговых фильтров. Кроме того, при этом преобразовании не сохраняется импульсная характеристика.
3. Частотные преобразования.
В предыдущих подразделах были рассмотрены три метода расчета цифровых фильтров. Во всех этих методах на первом этапе находится подходящий аналоговый фильтр, который удовлетворяет исходным требованиям. Расчет аналогового фильтра начинается с нахождения соответствующего аналогового фильтра-прототипа нижних частот. В дальнейшем используется подходящее частотное преобразование для перевода этого прототипа нижних частот в требуемый аналоговый фильтр. Наконец, на основе процедуры отображения этот аналоговый фильтр преобразуется в желаемый цифровой БИХ-фильтр, который удовлетворяет предъявленным требованиям. Процедура перехода на основе метода инвариантности импульсной характеристики по существу не обеспечивают хороших методов расчета цифровых фильтров, если полоса аналогового фильтра не ограничена низкими частотами. Метод билинейного преобразования (из-за нелинейного соотношения между цифровой и аналоговой частотой) дает лучшие результаты только для тех частотных характеристик аналогового фильтра, которые представляют собой ступенчатообразную функцию. Это означает, что такая процедура расчета не обеспечивает хороших методов расчета фильтров верхних частот, заграждающих и некоторых типов полосовых фильтров.
Для исключения этих недостатков используется другой подход к расчету цифровых БИХ-фильтров на основе методов расчета аналоговых фильтров. В этом случае процедура перехода всегда имеет дело с нормированным прототипом нижних частот. Следовательно, рассмотренные в предыдущих подразделах процедуры перехода смогут обеспечить хорошие результаты. В основном этот подход состоит в нахождении подходящего нормированного аналогового фильтра нижних частот. Аналоговый прототип отображается в цифровой фильтр-прототип нижних частот. Наконец, используется цифровое частотное преобразование для перехода от цифрового прототипа нижних частот к окончательному варианту, т. е. цифровому фильтру с подходящими характеристиками в полосе пропускания и полосе задерживания и удовлетворяющему предъявленным требованиям.
2.3.2. Расчет цифровых КИХ-фильтров.
Передаточная функция цифрового КИХ-фильтра представляется в виде
 , ,
| (33) |
где импульсная характеристика имеет длительность N. Если импульсная характеристика цифрового КИХ-фильтра удовлетворяет следующему условию:
| h (n)= h (N –l– n), | (34) |
для n =0, 1,..., (N /2)–1, когда N четное, и для n =0, 1,..., (N –1)/2, когда N нечетное, то цифровой фильтр будет обладать линейной фазовой характеристикой.
В большинстве случаев именно потребность в линейной фазе или постоянном групповом времени вызывает необходимость применения цифровых КИХ-фильтров.
1. Метод частотной выборки.
Заданный уравнением (33) цифровой КИХ-фильтр имеет эквивалентное ДПФ-преобразование вида:
 , ,
| (35) |
где – в действительности дискретизированная N -точечная частотная характеристика цифрового фильтра с равномерно расположенными отсчетами. Вследствие этого импульсная характеристика h (n) и передаточная функция Н (z) цифрового КИХ-фильтра определяется через ДПФ (35) таким образом:

| (36) |
| и. | (37) |
Уравнение (37) является основным при расчете цифрового КИХ-фильтра.
Предположим, что частотная характеристика Hd (e jq) задана для частот– p < q < p. Это означает, что она определена и для всех частот q. Процедура расчета должна давать значения, т. е. дискретизированную N -точечную требуемую частотную характеристику с равномерным расположением отсчетов:
 , при q =2 pk / N, , при q =2 pk / N,
| (38) |
где k =0, 1, 2, …, N –1. Используя непосредственно данные соотношения (38), можно получить подходящую КИХ-передаточную функцию из уравнения (37). Эта методика обеспечивает совпадение полученной и требуемой частотных характеристик в точках дискретизации q =2 pk / N для k =0, 1, 2,..., N –l.
2. Метод взвешивания.
Поскольку частотная характеристика Н (е jq) любого цифрового фильтра представляет собой периодическую функцию частоты q, она имеет разложение в ряд Фурье:
 , ,
| (39) |
где  . .
| (40) |
Очевидно, что коэффициенты ряда Фурье h (n) фактически представляют собой импульсную характеристику цифрового фильтра.
Одним из возможных способов получения цифровых КИХ-фильтров, аппроксимирующих функцию Н (е jq), является усечение бесконечного ряда (39) до конечного числа членов. Однако из хорошо известного явления Гиббса следует, что усечение бесконечного ряда вызывает выбросы и колебания в требуемой частотной характеристике до и после любой точки разрыва. Кроме того, величина этих выбросов и колебаний не уменьшается с увеличением длины последовательности при условии сохранения ее конечности. Это по существу означает, что прямое усечение уравнения (39) для получения аппроксимации цифрового КИХ-фильтра не обеспечивает хороших результатов.
Метод взвешивания используется для получения конечных весовых последовательностей w (n), называемых окнами, которые модифицируют коэффициенты Фурье в уравнении (39) для получения требуемой импульсной характеристики hd (n) конечной длительности, где:
| hd (n)= h (n) w (n), | (41) |
а w (n) – последовательность конечной длительности, т. е. w (n)=0 для n > N и n <0. Из соотношения (41) следует, что результирующая импульсная характеристика hd (n) также имеет протяженность N отсчетов.
Поскольку умножение двух последовательностей во временной области эквивалентно свертке двух частотных характеристик в частотной области, метод взвешивания обеспечивает сглаживание выбросов первоначальной частотной характеристики, т. е. подавление ее отклонений и пульсаций. Недостатком является расширение переходной полосы.
Для завершения этого подраздела приведем некоторые характерные функции окна:
а) прямоугольное окно:



б) окно Бартлетта или треугольное окно:



в) окно Ханна:



Как и в случае аналоговых фильтров, цифровые БИХ-фильтры не могут обеспечить совершенные линейные фазовые характеристики. В противоположность им цифровые КИХ-фильтры могут быть рассчитаны для обеспечения линейных фазовых характеристик. Кроме того, цифровые КИХ-фильтры всегда устойчивы. Это положительные качества цифровых КИХ-фильтров. К отрицательным чертам относится то, что исполнение цифрового КИХ-фильтра требует большего числа вычислений и большего числа цифровых элементов. Однако во многих ситуациях требуются цифровые КИХ-фильтры для выполнения тех задач, которые невозможно решить на основе цифровых БИХ-фильтров, а именно: получение фильтров с линейной фазой и многоскоростных фильтров, где входной и соответствующий выходной сигналы дискретизированы на разных скоростях.
2.3.3 Представление цифровых фильтров на z- плоскости.
Цифровой фильтр может быть синтезирован путем размещения полюсов и нулей передаточной функции на z- плоскости, основанном на следующих правилах:
1. Полюса и нули должны быть либо действительными, либо иметь комплексно-сопряженную пару.
2. Полюс в точке z=0 оказывает влияние на фазо-частотную характеристику фильтра и не изменяет амплитудно-частотную.
3. Полюс (или ноль) на единичной окружности означает, АЧХ на данной частоте бесконечно возрастает (или обращается в ноль).
4. Полюс вне единичной окружности означает, что фильтр нестабилен, т.е. отклик фильтра на импульс не затухает, а возрастает.


Амплитудно-частотная характеристика и представление на z- плоскости цифрового полосовой фильтр 6-го порядка, где:
• – ноль,  –полюс.
–полюс.
ИЗУЧЕНИЕ СВОЙСТВ И ПАРАМЕТРОВ ЦИФРОВЫХ ФИЛЬТРОВ
Целью работы является генерация сигнала, состоящего из нескольких гармоник, в системе MATLAB 6.1 и исследование в приложении Signal Processing Tool (SPTool) действия фильтров нижних, верхних частот, полосовых и режекторных фильтров на этот сигнал.
Первой задачей является генерация сигнала. Для этого запустите MATLAB 6.1. В начале создания некоторого сигнала зададим вектор-столбец времени t. Для этого в окне Command Window наберите строку:
>> t=(0:.01:2)’;
Эта команда задает изменение t от 0 до 2 с шагом 0,01 и обеспечивает дискретизацию сигнала по времени.
Теперь зададим вектор некоторой функции y(t), которая представляет собой сумму синусоиды с амплитудой 1 и частотой 1 Гц с синусоидой, имеющей амплитуду 0.25 и частоту 3 Гц:
>> y=sin(2*pi*1*t)+0.25*sin(2*pi*3*t);
Обратите внимание на то, что в этом выражении t – вектор, а потому и y тоже будет вектором. Частота f =1 Гц в первой компоненте сигнала указана в явном виде (как 1) только ради наглядности. Полезно учесть, что в большинстве расчетов MATLAB не использует размерные величины, поэтому лучше сразу привыкнуть к безразмерным величинам.
Теперь можно задать построение графика y(t):
>> plot(t,y);
Обрабатывать сигналы удобно используя приложение Signal Processing Tool (SPTool), которое вызывается следующей командой:
>> sptool
Чтобы импортировать сохраненный нами сигнал в это приложение выберите в меню File пункт Import… В раскрывшимся окне поставьте переключатель Source в положение From Workspace. В поле Workspace Contents выберите строку, в которой записано имя функции описывающей сигнал (в данном примере это y), и нажмите на верхнюю кнопку со стрелкой. В поле Sampling Frequency введите частоту дискретизации. Эта величина обратна шагу изменения времени t, заданному при формировании сигнала (в данном примере шаг изменения t равен 0,01, а частота дискретизации, следовательно, равна 100).

| (42) |
В поле Name записано имя, под которым будет значиться данный сигнал в приложении SPTool. На данной стадии это имя можно изменить по собственному усмотрению. Нажмите кнопку Ok.
Теперь в списке Signals наряду с именами встроенных сигналов появилось имя импортированного сигнала. Нажав кнопку View под списком Signals, можно посмотреть график выделенного сигнала.
В данном приложении можно проектировать и использовать цифровые фильтры для обработки сигналов. В списке Filters записаны имена трех встроенных фильтров. При нажатии кнопки View под списком Filters, появится окно Filter Viever. В нем можно посмотреть:
- АЧХ-фильтра (амплитуду можно задать либо в линейном, либо в логарифмическом масштабе либо в децибелах; частоту – либо в линейном, либо в логарифмическом масштабе);
- ФЧХ-фильтра (угол можно задать либо в радианах, либо в градусах; частоту – либо в линейном, либо в логарифмическом масштабе);
- групповое время задержки фильтра;
- нули и полюса фильтра;
- отклик на единичный импульс.
Нажав на кнопку New, получаем возможность проектирования фильтров. Кнопка Edit дает возможность редактировать ранее созданные фильтры. В раскрывшемся окне Filter Designer задаются параметры фильтра, производится расчет порядка фильтра и вывод АЧХ.
В поле Sampling Frequency введите частоту дискретизации обрабатываемого сигнала. В поле Algorithm можно выбрать один из следующих видов цифровых фильтров:
- КИХ-фильтр Ремеза;
- КИХ-фильтр с минимальным среднеквадратическим отклонением;
- КИХ-фильтр с окном Кайзера;
- БИХ-фильтр с аппроксимацией Баттерворта;
- БИХ-фильтр с аппроксимацией Чебышева;
- БИХ-фильтр с аппроксимацией инверсной Чебышева;
- БИХ-фильтр с эллиптической аппроксимацией.
Выбрав пункт Pole/Zero Editor можно задать с помощью мыши или вводя координаты на Z -плоскости полюса и нули передаточной функции.
Порядок фильтра либо рассчитывается (если стоит птичка в поле Minimum Order), если вводится в поле Order (если птичка снята). В данной работе порядок фильтров будет рассчитываться.
В поле Type задается тип фильтра: ФНЧ, ФВЧ, полосовой или режекторный фильтр.
Ниже вводятся граничные частоты и затухания полос пропускания и задерживания.
Все вносимые изменения будут тут же отображаться на графике, если поставить птичку в поле Auto Design.
Чтобы отфильтровать сигнал, выберите его в списке Signals, затем в списке Filters выберите фильтр и нажмите на кнопку Apply. В раскрывшимся окне введите (или оставьте введенное по умолчанию) имя отфильтрованного сигнала. Нажмите Ok. Теперь это имя добавилось в списке Signals. Посмотреть график отфильтрованного сигнала можно описанным выше способом.
Дата добавления: 2015-10-21; просмотров: 79 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Этап 1. Создаем основу будущего монстрика. | | | Задание |