Дифференциальная (разностная) фотометрия

На воспроизводимость результатов фотометрических измерений влияют:

• погрешности приготовления раствора;

• мутность, флуоресценция раствора;

• кюветные погрешности (использование кювет разной толщи­ны, невоспроизводимость положения кювет в кюветодержателе),

• сигнал фона;

• погрешности установки аналитической длины волны;

• погрешность спектрофотометрического измерения, вклю­чающая погрешности настройки прибора на 0 и 100% пропускания, нестабильность работы электронной схемы, погрешность отсчёта показаний прибора.

Не любые значения A и T можно измерить с одинаковой вос­производимостью. Если принять, что АТ (но не АА) является постоян­ной величиной во всём интервале значений Т, то зависимость AC/C от A при этом будет иметь вид, показанный на рис. 20.13. Математиче­ски можно показать, что минимум зависимости AC/C от A находится при А = 0,434 (T = 0,368).

aC/C.100%

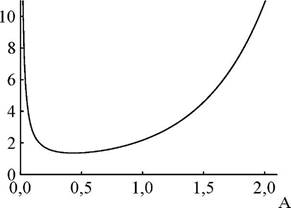Рис. 20.13. Зависимость относительной погрешности фотометрических определений от А (AT = 0,5%)

Оптимальный интервал измерения А и Т выбирают с таким рас­чётом, чтобы на всём его протяжении относительная погрешность из­мерения оптической плотности не превышала удвоенной минималь­ной относительной погрешности. Для условий, описанных выше, оп­тимальный интервал оптической плотности равен примерно 0,1-1,0. На самом деле погрешность отсчёта, например, у приборов с цифро­вой индикацией обычно не является основным фактором, вносящим вклад в общую воспроизводимость измерения A и Т. Значение А_опт за­висит от условий измерения и для большинства используемых спек­
трофотометров составляет 0,5-0,8, а рабочий интервал измерения рас­пространяется от 0,2 до 1,7. При работе на фотоэлектроколориметре диапазон рабочих значений оптической плотности сужается до 0,1-0,7.

В качестве раствора сравнения используется раствор с известной концентрацией вещества ^С 0 ^(С0 < ^Cx⁾ Используется при анализе растворов, имеющих большую оптическую плотность. метод отношения пропусканий I

При измерении слишком малых или слишком больших значений оптической плотности или пропускания погрешность измерения зна­чительно увеличивается. В спектрофотометрическом методе анализа существует целый ряд приёмов, которые были разработаны специаль­но для того, чтобы расширить диапазон определяемых концентраций и уменьшить погрешности измерения слишком малых или слишком больших величин Т и А. Эти приёмы спектрофотометрического ана­лиза получили название дифференциальной («разностной») спектро- фотометрии. Известно 3 разновидности дифференциальной фотомет­рии:

Нижняя граница шкалы j устанавливается по раствору j контрольного опыта, верхняя - по раствору с известной! концентрацией С (С > C_x)!

Используется при анализе! растворов, имеющих малую j оптическую плотность.!

метод анализа следов

~ I

ДИФФЕРЕНЦИАЛЬНАЯ ФОТОМЕТРИЯ

, I ~

метод предельной точности

Нижняя граница шкалы устанавливается по раствору С1, верхняя по С2 (С2 > C_x > C1)

Зависимость между концентрацией вещества в анализируемом растворе и наблюдаемой оптической плотностью в методе отношения пропусканий описывается формулой

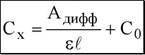
В методе анализа следов и методе предельной точности наблю­даемая величина оптической плотности нелинейно зависит от концен­трации определяемого вещества, поэтому определение концентрации проводится только методом градуировочного графика.

Многоволновая спектрофотометрия (метод Фирордта)

Данный приём спектрофотометрического анализа используется в том случае, если в растворе присутствуют несколько поглощающих веществ. В основе метода Фирордта лежит закон аддитивности опти­ческих плотностей. Пусть в растворе присутствуют два компонента.

Х

Оптическая плотность этого раствора при длине волны Х₁ равна A ¹,

х

а при длине волны Х₂ - A ². Составим систему из двух уравнений:

A^Х = (еХ¹ С₁ +SX¹ С₂) ■ I A^Х2 = (еХ²С₁ + еХ²С₂) ■ I

где е - молярные коэффициенты поглощения данных веществ при данных длинах волн (которые определяются заранее для растворов индивидуальных веществ).

Если решить данную систему уравнений, то можно найти неиз­вестные концентрации C₁ и С₂.

Если в растворе присутствуют не два, а n поглощающих веществ, то для расчёта их концентраций необходимо иметь не менее n-уравнений, для чего тре­буется измерять оптическую плотность не менее, чем при n-длинах волн. Для обработки полученных сложных систем уравнений существуют специальные математические приёмы.

Метод Фирордта может быть использован лишь в том случае, если поглощение всех веществ, входящих в состав смеси, а также сме­си в целом подчиняется основному закону светопоглощения.

Дата добавления: 2015-09-07