Студопедия
Случайная страница | Главная
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Определение напряжений, возникающих в поперечных сечениях бруса при прямом поперечном изгибе. Вывод формулы Д.И. Журавского.

Читайте также:
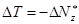  1. I.2 Определение понятия фразеологизма
  2. III. Выводы
  3. III. Выводы
  4. III. Выводы или резюме
  5. III. ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНОСТИ ПРОИЗВОДСТВА
  6. А) Определение расчетных усилий в ветвях колонны
  7. А) Определение требуемой площади поперечного сечения колонны.

(1)

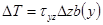(2)

,

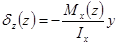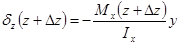
(3) – статический момент отсечённой части площади поперечного сечения относительно оси х (нейтральной линии).

Подставим в (1), (2), (3):

,

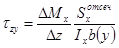
- формула Журавского для вычисления касательных напряжений в поперечном сечении балки при прямом поперечном изгибе.

 

Сравнительная оценка максимальных нормальных и максимальных касательных напряжений при прямом поперечном изгибе бруса.

,

,

.

 

Условие прочности при прямом поперечном изгибе бруса.

,

.

 

Вывод формул для вычисления касательных напряжений в брусе прямоугольного и двутаврового поперечного сечения с использованием формулы Д.И. Журавского.

Расчёт касательных напряжений в прямоугольном поперечном сечении балки с использованием формулы Д.И.Журавского:

, .

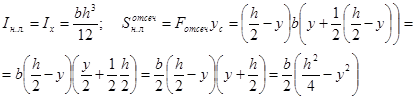
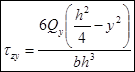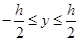при у=0

при .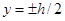

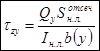
Iн.л.=Ix – находится по таблице.

b(y)=d – находится по таблице.

,

.

 

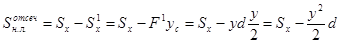
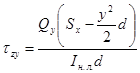
Дата добавления: 2015-09-06; просмотров: 234 | Нарушение авторских прав

Читайте в этой же книге: Дайте определение полного, нормального и касательного напряжений. | Вывод формул обобщенного закона Гука. | Интегральные выражения для геометрических характеристик плоской фигуры. | Вывод формулы для определения потенциальной энергии упругой деформации при изгибе бруса в статическом режиме нагружения. | Вывод формулы Эйлера. | Условие применимости формулы Эйлера. | Формула Ясинского. | Определение допускаемой силы на устойчивость. | Кривая Веллера. Определение предела выносливости. Предел выносливости образца и детали. Основные факторы, влияющие на предел выносливости детали. | Определение коэффициента запаса усталостной прочности при совместном действии изгиба и кручения бруса. Формула Гаффа-Полларда (без вывода). |
<== предыдущая страница | следующая страница ==>
Определение моментов инерции сложных плоских фигур.| Вывод упрощенного дифференциального уравнения изогнутой оси бруса. Определение абсолютных линейных и угловых перемещений при изгибе бруса.
mybiblioteka.su - 2015-2025 год. (0.107 сек.)