Вывод формулы Эйлера.

Выбрав начало координат в точке А и направление координатных осей, как показано на рис.3, имеем:

(1)

деля обе части уравнения на EJ и обозначая дробь через приводим его к виду:

Общий интеграл этого уравнения имеет вид:

Это решение заключает в себе три неизвестных: постоянные интегрирования а и b и значение , так как величина критической силы нам неизвестна.

Краевые условия на концах стержня дают два уравнения:

в точке А при х = 0 прогиб у = 0,

В х = 1 у = 0.

Из первого условия следует (так как и cos kx =1)

0 = b.

Таким образом, изогнутая ось является синусоидой с уравнением

(2)

Применяя второе условие, подставляем в это уравнение

у = 0 и х = l

получаем:

Отсюда следует, что или а или kl равны нулю.

Если а равно нулю, то из уравнения (2) следует, что прогиб в любом сечении стержня равен нулю, т. е. стержень остался прямым. Это противоречит исходным предпосылкам нашего вывода. Следовательно, sin kl = 0, и величина может иметь следующий бесконечный ряд значений:

где — любое целое число.

Отсюда , а так как то

и

Первый корень =0 требует, чтобы было равно нулю, что не отвечает исходным данным задачи; поэтому этот корень должен быть отброшен и наименьшим корнем принимается значение 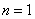. Тогда получаем выражение для критической силы:

(3)

(Здесь J —минимальный момент инерции поперечного сечения стержня.) Это — так называемая формула Эйлера для сжатого стержня с шарнирно-опертыми концами. Значению критической силы (3) соответствует изгиб стержня по синусоиде с одной полуволной [формула (2)]

Дата добавления: 2015-09-06