Дайте определение полного, нормального и касательного напряжений.

Напряжение – мера распределения внутренних сил по сечению.

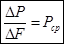, где 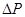- внутренняя сила, выявленная на площадке .

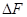Полное напряжение .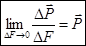

Нормальное напряжение – проекция вектора полного напряжения на нормаль обозначается через σ. 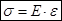, где Е – модуль упругости I рода, ε – линейная деформация. Нормальное напряжения вызывается только изменением длин волокон, направлением их действий, а угол поперечных и продольных волокон не искажается.

Касательное напряжение – составляющие напряжения в плоскости сечения. 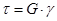, где (для изотропного материала) – модуль сдвига (модуль упругости II рода), μ – коэффициент Пуассона (=0,3), γ – угол сдвига.

1. Какая деформация называется абсолютной, относительной, линейной и угловой?

Линейная деформация характеризует изменение размеров тела. Различают абсолютную деформацию ΔL и относительную деформацию ε = ΔL/L.

Угловая деформация характеризует изменение формы тела и чаще всего называется углом сдвига.

Угол сдвига — это изменение первоначально прямого угла. γ = α + β.

Полная деформация — это сумма линейной и угловой деформации.Если взять малый элемент тела параллелепипед, ориентированный по осям x, y, z, то соответственно возникает три линейных деформации (вдоль осей x, y, z) ε_x,ε_y, ε_z

x = dx Δ dx y = dy Δ dy z = dz Δ dz

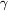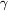и три угловые деформации xy yz 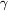zx в трех взаимно-перпендикулярных плоскостях.

Относительные линейные и угловые деформации – величины безразмерные. Абсолютная деформация выражает абсолютное изменение какого-либо линейного или углового размера, площади сечения или участка граничной поверхности элемента, выделенного в деформируемом теле, или всего тела. Относительная деформация характеризует относительное изменение тех же величин. Обычно относительную деформацию определяют как отношение абсолютного изменения какого-либо размера к его первоначальному значению. Абсолютная деформация при осадке ∆ H = H - h. не характеризует степени воздействия деформации на металл. Относительную деформацию в процентах для обеих заготовок подсчитаем по формуле є= (H-h') / H*100

1. Какой вид нагружения бруса называется центральным растяжением-сжатием?

Центральным растяжением (или центральным сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние усилия равны нулю. Иногда центральное растяжение (или центральное сжатие) кратко называют растяжением (или сжатием).

1. Вывод формул для определения напряжений, возникающих в поперечных и наклонных сечениях бруса при центральном растяжении-сжатии.

1. Условие прочности при центральном растяжении-сжатии. Три типа задач на прочность.

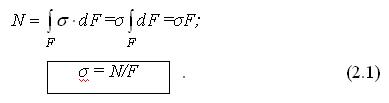
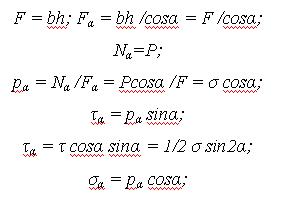
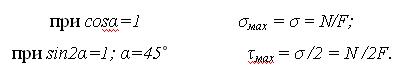
Условие прочности: σ ≤[ σ]

Три типа задач;

1)Проверочный расчет

а)для хрупких материалов

[σ_сжат]=(3….5)·[σ_растяж]

Условия прочности

|мах.σ_сжат|≤[σ_сжат]

|махσ_растяж|≤[σ_растяж]

Проверяем мах. сжатое и мах. растянутое волокно;

max σ_сжат=М(х)у_мах^сжат/J_z=M(x)/W_z, W_z=J_z/y_мах^сжат

у_мах^сжат-мах расстояние от нейтральной оси до сжатого волокна

W_c-момент сопротивления сжатия поперечного сечения

Maxσ_растяж=М(х)у_мах^растяж/J_z=M(x)/W_z^растяж

W_Z^раст-момент сопротивления растяжения поперечного сечения

в)Для пластичных материалов

[σ_сж]=[σ_р]=[σ]

2)Проэктный расчет

Из условия прочности σ=М(х)/W≤[σ]

W_Z≥М(х)/[σ], W_Z-момент сопротивления поперечного сечения

W_Z=J_Z/y_max

а) для прямоугольного сечения

W_Z=J_Z/y_max, J_Z=bh³/12,

y_max=h/2 b) для круглого сечения

W_Z=J_Z/y_max, J_Z=пd⁴/64, y_max=d/2

c) для двутавра

Рассчитываем по формуле W_Z

W_Z=|M_max|/[σ]

M _max-из эпюра

Выбираем из таблицы больший и меньший двутавр, и с помощью табличных значений W_Z для выбранных двутавров рассчитываем σ и сравниваем с [σ]. Подходящий тот двутавр, которого σ удовлетворяет условия прочности. Так же сравниваем с условием рациональности по формуле |σ-[σ]/[σ]|·100%≤5%, отклонение не должно превышать 5%.

1. Закон Гука для случая одноосного напряженного состояния.

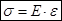- закон Гука для одноосного напряжённого состояния в точке.

Е – коэффициент пропорциональности (модуль упругости I рода). Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и σ, т.е. в кГ/см².

1. Определение деформаций и перемещений при центральном растяжении-сжатии.

Центральное напряжение (сж.) .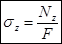

При центральном растяжении (сж.) бруса в поперечном направлении в сечении возникает только нормальное напряжение σ_z, постоянное во всех точках поперечного сечения и равное N_z/F. 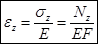, где EF – жёсткость бруса при растяжении (сжатии). Чем больше жёсткость бруса, тем меньше деформируется бус при одной и той же силе. 1/(EF) – податливость бруса при растяжении (сжатии).

13.Диаграмма растяжения малоуглеродистой стали. Прочностные и деформационные характеристики стали. Наклёп.

Обычно диаграмма растяжения является зависимостью приложенной нагрузки P от абсолютного удлинения Δl. Современные машины для механических испытаний позволяют записывать диаграмму в величинах напряжения σ (σ = P/A₀, где A₀ — исходная площадь поперечного сечения) и линейной деформации ε (ε = Δl/l₀). Такая диаграмма носит название диаграммы условных напряжений, так как при этом не учитывается изменение площади поперечного сечения образца в процессе испытания.

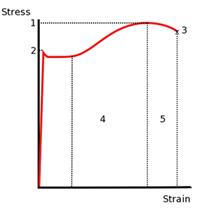
Рис. 1. Типичная диаграмма σ — ε для малоуглеродистой стали

1. Предел прочности (временное сопротивление разрушению)
2. Предел текучести (верхний)
3. Точка разрушения
4. Область деформационного упрочнения
5. Образование шейки на образце

Начальный участок является линейным (т. н. участок упругой деформации). На нём действует закон Гука:

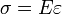
Затем начинается область пластической деформации. Эта деформация остаётся и после снятия приложенной нагрузки. Переход в пластическую область обнаруживается не только по проявлению остаточных деформаций, но и по уменьшению наклона кривой с увеличением степени деформации. Данный участок диаграммы обычно называют площадкой (зоной) общей текучести, так как пластические деформации образуются по всей рабочей длине образца. С целью изучения и точного анализа диаграммы деформации, современные испытательные машины оснащены компьютеризированной записью результатов.

По наклону начального участка диаграммы рассчитывается модуль Юнга. Для малоуглеродистой стали наблюдается т. н. «зуб текучести» и затем площадка предела текучести. Явление «зуба» текучести связано с дислокационныммеханизмом деформации. На начальном участке плотность дислокаций является недостаточной для обеспечения более высокой степени деформации. После достижения точки верхнего предела текучести начинается интенсивное образование новых дислокаций, что приводит к падению напряжения. Дальнейшая деформация при пределе текучести происходит без роста напряжения 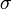. Зависимость предела текучести, 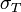от размера зерна, d, выражена соотношением Петча-Холла:

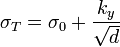
После достижения конца площадки текучести (деформация порядка 2 — 2,5 %) начинается деформационное упрочнение (участок упрочнения), видимое на диаграмме, как рост напряжения с ростом деформации. В этой области до достижения максимальной нагрузки (напряжения (σ_В) макродеформация остаётся равномерной по длине испытуемого образца.

14. Что называется модулем упругости первого рода? Какова его размерность, физический и геометрический смысл?

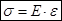- закон Гука для одноосного напряжённого состояния в точке.

Е – коэффициент пропорциональности (модуль упругости I рода). Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и σ, т.е. в кГ/см².

15. Что называется коэффициентом Пуассона? Пределы изменения коэффициента Пуассона для изотропного, однородного материала.

μ – коэффициент Пуассона (коэффициент пропорциональности). 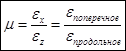. Безразмерная величина, характеризующая свойства материала и определяющаяся экспериментально и лежит в интервале от 0,25 до 0,35

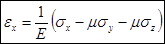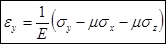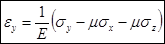, , . Сложив эти уравнения, получим выражение объёмной деформации: 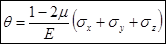. Это выражение позволяет определить предельное значение коэффициента Пуассона для любого изотропного материала. Рассмотрим случай, когда σ_x=σ_y=σ_z=р. В этом случае: 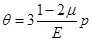. При положительном р величина θ должна быть также положительной, при отрицательном р изменение объёма будет отрицательным. Это возможно только в том случае, когда μ≤1/2. Следовательно, значение коэффициента Пуассона для изотропного материала не может превышать 0,5.

Дата добавления: 2015-09-06