Вывод формул обобщенного закона Гука.

Наряду с увеличением размеров в направлении действия; же напряжения происходит уменьшение размеров в двух ортогональных направлениях (рис. 1). Соответствующие деформации обозначим через 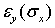и , причем эти деформации отрицательны при положительных и пропорциональны :

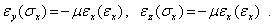
(2)

Коэффициент пропорциональности 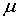называется коэффициентом Пуассона, который в силу изотропности материала одинаков для обоих ортогональных направлений.

Соотношения, аналогичные (1) и (2), в случае одноосного нагружения в направлении осей Оу, Ог напряжением 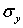, , 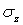соответственно имеют вид

	(3)
	(4)

При одновременном действии напряжений по трем ортогональным осям, когда отсутствуют касательные напряжения, для линейно-упругого материала справедлив принцип суперпозиции (наложения решений):

С учетом формул (1 — 4) получим

(5)

Касательные напряжения вызывают угловые деформации, причем при малых деформациях они не влияют на изменение линейных размеров, и следовательно, на линейные деформации. Поэтому они справедливы также в случае произвольного напряженного состояния и выражают так называемый обобщенный закон Гука.

19. Что называется модулем упругости второго рода? Соотношение между тремя упругими постоянными изотропного, однородного материала (без вывода).

(для изотропного материала) – модуль сдвига (модуль упругости II рода), μ – коэффициент Пуассона (=0,3), γ – угол сдвига.

, , .

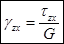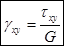Дата добавления: 2015-09-06