Группоиды, полугруппы, группы

Группоид — множество с одной бинарной операцией , обычно называемой 0%A3%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5"умножением.

Правая квазигруппа — группоид, в котором возможно правое деление, то есть уравнение имеет единственное решение для любых a и b.

Квазигруппа — одновременно 0%9F%D1%80%D0%B0%D0%B2%D0%B0%D1%8F_%D0%BA%D0%B2%D0%B0%D0%B7%D0%B8%D0%B3%D1%80%D1%83%D0%BF%D0%BF%D0%B0"правая и левая квазигруппы.

Лупа — квазигруппа с единичным элементом , таким, что .

Полугруппа — группоид, в котором умножение 0%90%D1%81%D1%81%D0%BE%D1%86%D0%B8%D0%B0%D1%82%D0%B8%D0%B2%D0%BD%D0%BE%D1%81%D1%82%D1%8C"ассоциативно: .

Моноид — полугруппа с единичным элементом.

Группа — моноид, в котором для каждого элемента a группы можно определить обратный элемент a ⁻¹, такой, что .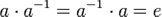

Абелева группа — группа, в которой операция 0%9A%D0%BE%D0%BC%D0%BC%D1%83%D1%82%D0%B0%D1%82%D0%B8%D0%B2%D0%BD%D0%BE%D1%81%D1%82%D1%8C"коммутативна, то есть, . Операцию в абелевой группе часто называют сложением ('+').

Кольца

Полукольцо — похоже на кольцо, но без обратимости сложения.

Почти-кольцо — также обобщение кольца, отличающееся от обычного кольца отсутствием требования коммутативности сложения и отсутствием требования дистрибутивности умножения по сложению (левой или правой)

Кольцо — структура с двумя бинарными операциями: абелева группа по сложению, моноид по умножению, выполняется закон 0%94%D0%B8%D1%81%D1%82%D1%80%D0%B8%D0%B1%D1%83%D1%82%D0%B8%D0%B2%D0%BD%D0%BE%D1%81%D1%82%D1%8C"дистрибутивности: .

Коммутативное кольцо — кольцо с коммутативным умножением.

Целостное кольцо — кольцо, в котором произведение двух ненулевых элементов не равно нулю.

Тело — кольцо, в котором ненулевые элементы образуют группу по умножению.

Поле — коммутативное кольцо, являющееся телом.

Дата добавления: 2015-09-06