Определение криволинейного интеграла первого рода. Свойства

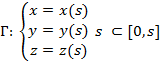-естественная параметризация

Г-

Г+

Опр. F(s)=F(x(s),y(s),z(s)) на [0,s] интегрируема тогда 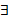криволинейные интегралы первого рода от F по Г и *( ; *()=

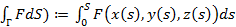Г-: ,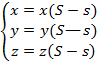

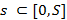
0=s₀<s₁<…<s_n=S

длина

t_j 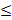[s_j-1,s_j], j=1..n

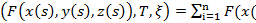t_j),y(t_j),z(t_j))(s_j-s_j-1)

Криволинейные интегралы второго рода. Свойства

Г гладкая(кусочно гладкая)

a( )=(P(xyz),Q(xyz),R(xyz))

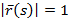
Опр. ; 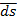:= (s)ds

Если 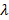кусочно гладкая, то ;

-циркуляция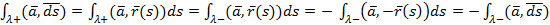

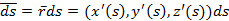
P: 0=s₀<s₁<…<s_n=S; [s_j-1,s_j]

	выбираем , так чтобы ()

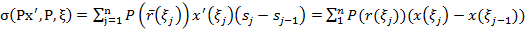
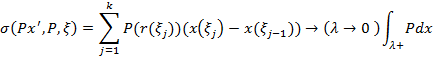
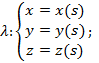
(x(0),y(0),z(0))=()

Формула Грина. Случай элементарной области.

  d C c A B a b

, G односвязна в D. D(xy), Q(xy), dP/dy, dQ/dx непрерывны. dG кусочно гладкая. Тогда

Доказательство при дополнительных ограничениях на G

а) G криволинейный треугольник

AB||Ox, AC||Oy, AC-график непрерывной строго возрастающей функции y= 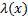,x

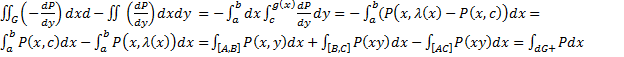
AC- график непрерывной строго возр. ф-ии

Дата добавления: 2015-10-13