Доказательство. Mkl:=supRklf(x,y), mkl:=intRklf(x,y)

R на R_kl

a=x₀<x₁<<x_n=b

c=y0<y₁<y_p=d

R_kl } k=1..n, l=1..p;

M_kl:=sup_Rklf(x,y), m_kl:=int_Rklf(x,y)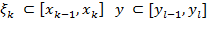

m_kl M_kl ; m_kl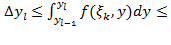

Складываем по l от 1 до Ф

Суммируем по k

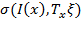; ()**= ; ()*=()***=S_T(f)

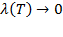
Замечание

Если 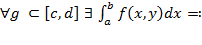I₂(y), то I₂(y) интегрируема на [c,d]и

Сведение двойного интеграла к повторному. Общий случай

Теор: G ограниченная замкнутая область. Проекция G на Ox – [ab] 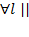Oy и пересекает [a,b]. l 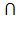G промежуток[y_H(x),y_b(x)]

сходится

Доказательство

R=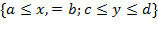

F(x,y):={ }

; *()=F(x,y)

(;

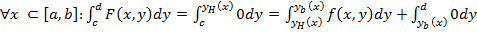
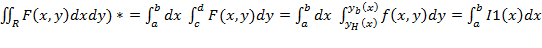Замечание 1

[c,d] проекция G на Oy. Если 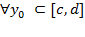G пересекается с y=y₀ по промежутку [x_n(y₀),x_t(y₀)] и 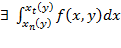, то

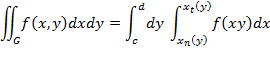
Определение тройного интеграла. Формулы замены переменных и повторного интегрирования для тройного интеграла.

Кубируемые области. Элементарные области: конечное объединение прямоугольных параллелепипедов с ребрами, параллельными осям координат без общих внутренних точек.

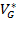- верхний объем G

; P-элементарно;

V_*G – нижний объем G

V_*G=supV(p); P –элементарно, P G

G кубируемо если 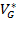= V_*G

Дата добавления: 2015-10-13