Условия независимости криволинейного интеграла второго рода от пути интегрирования

12 Условия независимости криволинейного интеграла второго рода от пути интегрирования для односвязной области

Пусть в области D заданы непрерывные функции P(x,y) и Q(x,y) и M₀M – гладкая дуга, лежащая в области D.

Рассмотрим вопрос о независимости интеграла от формы пути интегрирования. Место имеет следующая теорема:

Теор. Пусть функции P,Q,P’_Y,Q’_X определены и непрерывны в односвязной ограниченной замкнутой области D в плоскости Oxy. Тогда следующие четыре условия равносильны между собой:

1) , где L- замкнутый контур в области D;

2) Интеграл не зависит от формы пути интегрирования, а зависит лишь от положения точек M₀ и M.

3) Pdx+Qdy=dU- полный дифференциал некоторой функции U(x,y)

4) dQ/dx=dP/dy в каждой точке области D

1=>2

2=>3

Пусть A(x₀,y₀), является функцией от x,y, т.е.

u(x,y) = . Чтобы показать дифференцируемость u(x,y) т.е. du=Pdx+Qdy, достаточно доказать для По определению частной производной:

, где т.С( можно взять прямолинейным y=const. Тогда

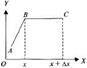И по теореме о среднем для определенного интеграла получаем

Аналогично доказывается равенство du/dy

3=>4 Из условия 3 следует, что по теореме о равенстве частных производных высших порядков, отличающихся порядком дифференцирования,

4=>1

Пусть гладкая замкнутая кривая L*D ограничивает область

Тогда по формуле Грина

13.Касательная плоскость и нормаль к явно заданной поверхности. Достаточное условие существования невертикальной касательной плоскости

Если поверхность задана явно: z = f(x; у), то в точке X₀(x₀; y₀; z₀) она обладает касательной плоскостью

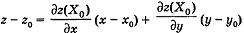
и нормалью

14. Понятие гладкой поверхности

Задание поверхности уравнением z=f(x,y)) (1) or x=f(y,z) (2) or y=f(x,z) (3)называется явным

Задание поверхности уравнением z=f(x,y,z) называется неявным

-параметрическое задание

Опр.

Пусть поверхность Ф задана явно, либо неявно, либо параметрически. Будем называть поверхность Ф гладкой, если для любой ее точки существует такая окрестность, которая вырезает часть поверхности Ф, допускающую явное представление любого вида(1,2,3), где f- непрерывно дифференцируемая функция

Если поверхность Ф задана явно уравнением (1) и функция f(x, y) непрерывно

дифференцируема в области G, то поверхность, очевидно, является гладкой.

Пусть поверхность Ф задана неявно уравнением (1) и пусть функция F(x, y, z) непрерывно дифференцируема. Точка М0(x0, y0, z0) поверхности Ф называется неособой, если в этой точке Fx2 + Fy2 + Fz2 ≠ 0. В противном случае точка называется особой. Если поверхность не содержит особых точек, то она является гладкой.

15. Касательная плоскость и нормаль к поверхности, заданной параметрически

Пусть поверхность Ф задана параметрически уравнениями (x = ϕ(u, v), y = ψ(u, v), z = χ(u, v), (u, v) ∈ g,), или, что то же самое,

уравнением (r = ϕ(u, v) i + ψ(u, v) j + χ(u, v) k, (u, v) ∈ g,). Точка M₀(ϕ(u, v), ψ(u, v), χ(u, v)) называется неособой точкой поверхности Ф, если в этой точке векторы

ru = i ϕ_u(u, v) + j ψ_u(u, v) + k χ_u(u, v),

rv = i ϕ_v(u, v) + j ψ_v(u, v) + k χ_v(u, v), неколлинеарны (линейно независимы). В противном случае точка M₀ называется особой. Простая поверхность, не имеющая особых точек, является гладкой.

Уравнение касательной плоскости к поверхности Ф в неособой внутренней точке M(ϕ(u,v), ψ(u, v), χ(u, v)) имеет вид A(x − x0) + B(y − y0) + B(М0)(z − z0) = 0.

где x0 = ϕ(u, v), y0 = ψ(u, v), z0 = χ(u, v),

Вектор N = [ru · rv] = i A + j B + k. С есть вектор нормали к поверхности Ф в точке M.

Векторы ru и rv, отложенные от точки M, лежат в касательной плоскости (рис).

16. Определение площади поверхностей, заданных в явном виде и параметрически

17

Дата добавления: 2015-10-13