
Читайте также:
|
Опр. 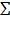 Uk, Uk ϵ ℝ (ℂ) сходится абсолютно если сходится
Uk, Uk ϵ ℝ (ℂ) сходится абсолютно если сходится 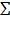 |Uk|
|Uk|
Утв. Если ряд сходится абсолютно, то он сходится.
Док. К. Коши( 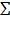 Uk сходится ó∀ ε>0 ∃N; ∀n≥N; ∀ p |
Uk сходится ó∀ ε>0 ∃N; ∀n≥N; ∀ p |  k|<ε)
k|<ε)
По к. Коши ∀ε>0 ∃N: ∀n>N ∀p |  k||(<ε)=
k||(<ε)=  k|≥|
k|≥|  k|(по нер-ву
k|(по нер-ву 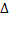 )
)
Т.е. для ряда 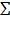 Uk Выполнен К.Коши.
Uk Выполнен К.Коши.
Лемма: ряд  k, Uk ≥0 сходится. Тогда при ∀ перестановке членов сходимость остается и сумма не меняется.
k, Uk ≥0 сходится. Тогда при ∀ перестановке членов сходимость остается и сумма не меняется.
Док-во.
 k’ –перестановка
k’ –перестановка  k. Проверяем ограниченность Sn’=
k. Проверяем ограниченность Sn’=  k’
k’
∀n Sn’=  k’
k’
K0- номер U0’ в исходном ряде.
K1- номер U1’ в исходном ряде.
,,,
Kn- номер Un’ в исходном ряде.
N=max{k0,k1,…,kn}
Sn’=  ’k ≤
’k ≤  k≤
k≤  k≤S ⇒Sn’ сходится ó сходится
k≤S ⇒Sn’ сходится ó сходится  k’=S’ ⇒S’≤S
k’=S’ ⇒S’≤S
После перестановки Сумма ряда не увеличивается. При обратной перестановке S≤S’⇒S=S’
Теорема: если ряд сходится абсолютно, то при любой перестановке его членов сходимость сохраняется и сумма ряда не меняется.
1) ∀k Uk ϵ ℝ
Uk+:={Uk если Uk≥0, 0 если Uk<0 } Uk-:={-Uk если Uk<0, 0 если Uk≥0 }
∀k Uk=Uk++Uk- ∀k |Uk|≥Uk+≥0 |Uk|≥Uk-≥0
Т.к. ряд 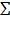 |Uk| сходится то по признаку сравнения Uk+и Uk- тоже сходятся.
|Uk| сходится то по признаку сравнения Uk+и Uk- тоже сходятся.
 k=
k=  k+-
k+-  k- =
k- =  k+-
k+-  k-=
k-=  k+-Vk-)=
k+-Vk-)= 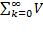 k
k
Где  k – переставленный ряд
k – переставленный ряд 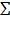 Uk
Uk 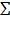 Vk+ и
Vk+ и 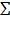 Vk- аналогично.
Vk- аналогично.
 k+-
k+-  k- Сходятся по Лемме
k- Сходятся по Лемме
2) ∀k Uk ϵ ℂ Пусть ∀k Uk=αk+Iβk;αk=ReUk βk=ImUk
∀k: |αk|≤|Uk| и |βk|≤|Uk| ⇒ 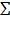 αk и
αk и 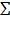 βk сходятся абсолютно (признак сравнения)
βk сходятся абсолютно (признак сравнения)
Пусть после перестановки получаем Vk=pk+iqk
 k=
k=  k+Iβk)=
k+Iβk)=  k+
k+  k=
k=  k +i
k +i 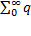 k=
k= 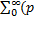 k+iqk)=
k+iqk)=  k
k
Опр.  k сходится условно если
k сходится условно если 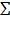 |Uk| расходится а
|Uk| расходится а 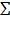 Uk сходится.
Uk сходится.
Умножение абсолютно сходящихся рядов.
Теорема: Пусть  k и
k и  k сходятся абсолютно. {Wk} – произвольным образом занумерованные произведения UkVm все и по 1 разу. Тогда
k сходятся абсолютно. {Wk} – произвольным образом занумерованные произведения UkVm все и по 1 разу. Тогда  k сходится абсолютно и его сумма
k сходится абсолютно и его сумма  k=
k=  k
k  k
k
Доказательство: Канторов диагональный процесс:
Занумеровать произведение можно.
1) 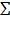 Wk Сходится абсолютно.
Wk Сходится абсолютно.
∀N  k ∀k Wk=UnkVmk
k ∀k Wk=UnkVmk
Пусть M≔ max{n1m1,n2m3, …, nNmN}
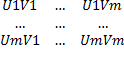 матрица MxM содержатся все слагаемые
матрица MxM содержатся все слагаемые 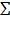 Wk
Wk
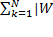 k|≤
k|≤  k|
k|  k|≤
k|≤ 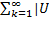 k|
k| 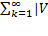 k| Т.е. честичные суммы ряда
k| Т.е. честичные суммы ряда 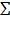 |Wk| ограничены ⇒ сходится
|Wk| ограничены ⇒ сходится 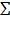 Wk абсолютно. ⇒ нумерацию можно выбирать произвольно исходя из удобства.
Wk абсолютно. ⇒ нумерацию можно выбирать произвольно исходя из удобства.

Sn2=  k
k 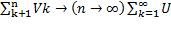 k
k  k
k
Sm имеет предел Sm→  k
k  k
k
8
Неравенство Абеля
аk монотонна ∃B ∀k |Bk|<B ∀k=1,…,n тогда: | 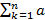 kbk|≤2B(|a1|+2|an|)
kbk|≤2B(|a1|+2|an|)
доказательство: (в разработке)
Признак Абеля.
{an} монотонна и ограничена. А 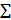 bn сходится. Тогда сходится
bn сходится. Тогда сходится 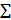 anbn
anbn
Доказательство: M:∀n ∀n |an|<M
∀ε>0 ∃N; ∀n≥N ∀p |  k|≤
k|≤ 
(Выполнено для каждой суммы ∀ l |  k|поэтому это В из нер-ва Абеля)
k|поэтому это В из нер-ва Абеля)
∀n≥N ∀p |  kbk|≤
kbk|≤ 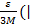 an+1|+2|an+p|)<ε
an+1|+2|an+p|)<ε  an+1|<M и|an+p|<M)
an+1|<M и|an+p|<M)
Признак Дирихле
{ak} монотонна и ak→0 при k→0 и частичные суммы  k ограничены. Тогда
k ограничены. Тогда 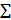 akbk сходится.
akbk сходится.
Доказательство:
Пусть Bn=  k; |Bn|≤B
k; |Bn|≤B
|  k|=|
k|=| 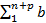 k -
k -  k |≤|
k |≤| 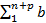 k |+|
k |+|  k |≤2B
k |≤2B
∀ε >0 ∃N ∀n≥N |an|< 
|  kbk|≤2B
kbk|≤2B  an+1|+2|an+p|)<2B(
an+1|+2|an+p|)<2B( ε
ε
(Признак Лейбница- частный случай признака Дирихле)
Сходимость и равномерная сходимость функциональных рядов и последовательностей. К. Коши равномерной сходимости. Необходимое условие равномерное сходимости функционального ряда. Признак Вейерштрасса равномерной сходимости функционального ряда.
{fn(x)} (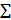 Uk(x)) сходится на 𝕏 Если ∀x0 ϵ 𝕏 числовая последовательность {f(x0)}(числовой ряд
Uk(x)) сходится на 𝕏 Если ∀x0 ϵ 𝕏 числовая последовательность {f(x0)}(числовой ряд 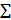 Uk(x0)) сходится.
Uk(x0)) сходится.
Поточечная сходимость
Пусть  — последовательность функций вида
— последовательность функций вида  (
( ) где
) где  — область определения, единая для всех функций семейства.
— область определения, единая для всех функций семейства.
Зафиксируем точку 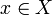 и рассмотрим числовую последовательность вида
и рассмотрим числовую последовательность вида  .
.
Если у этой последовательности имеется (конечный) предел, то точке  можно сопоставить предел этой последовательности, обозначив его
можно сопоставить предел этой последовательности, обозначив его  :
:
 .
.
Если рассмотреть всё точки множества  , в которых указанный предел существует, то можно определить функцию
, в которых указанный предел существует, то можно определить функцию  .
.
Таким образом определённая функция называется поточечным пределом последовательности функций семейства  на множестве
на множестве  :
:
 ,
,
а про само семейство  говорят, что оно поточечно сходится к функции
говорят, что оно поточечно сходится к функции 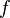 на множестве
на множестве  .
.
Равномерная и неравномерная сходимость:
Просто сходимость: "для каждой точки существует такой номер, что..."
Равномерная сходимость: "существует такой номер, что для каждой точки..." 








 Критерий Коши равномерной сходимости ряда.
Критерий Коши равномерной сходимости ряда.
неравномерно равномерно
{fn(x)} сходится не 𝕏 равномерно ó∀ε>0 ∃N=N(ε); ∀n≥N ∀p:
|fn+p(x)-fn(x)|<ε ∀x ϵ 𝕏;
Доказательство: ⇒) fn(x)⇒ f(x) на 𝕏 ∀ε>0 ∃N:∀n≥N:|fn(x)-f(x)|<  ; ∀x ϵ 𝕏
; ∀x ϵ 𝕏
∀p |fn+p(x)-fn(x)|=|((fn(x)-f(x))-(fn(x)-f(x))|≤ |((fn(x)-f(x))|+|(fn(x)-f(x))|≤  = ε;∀xϵ𝕩
= ε;∀xϵ𝕩
⇐) Если взять ∀x0 ϵ 𝕏 и зафиксировать его, то послед. {f(x0)} фундаментальна ⇒ {f(x0)} сходится(К. Коши). Обозначим f(x) поточечный предел {fn(x)} fn(x)→f(x) на 𝕏
∀ε >0 ∃N: ∀n≥N; ∀p |fn+p(x)-fn(x)|<  ∀x ϵ 𝕏
∀x ϵ 𝕏
X и n пока что зафиксированы. При p→∞ fn+p(x)→f(x) |f(x)-fn(x)|≤  <ε ⦆
<ε ⦆
К. Коши равномерной сходимости для ряда:
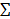 Uk(x) сходится на 𝕏 равномерно ó ∀ε>0 ∃N=N(ε) ∀n≥N, ∀p
Uk(x) сходится на 𝕏 равномерно ó ∀ε>0 ∃N=N(ε) ∀n≥N, ∀p
| 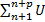 k(x)|<ε ∀x ϵ 𝕏;
k(x)|<ε ∀x ϵ 𝕏;
Следствие: необходимое условие равномерной сходимости ряда
Если 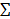 Uk(x) сходится на 𝕏 равномерно, то Uk(x)⇒0 на 𝕏
Uk(x) сходится на 𝕏 равномерно, то Uk(x)⇒0 на 𝕏
Док-во из К. Коши при p=1.
Дата добавления: 2015-10-13; просмотров: 98 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Перечень выбранного оборудования | | | Достаточное условие равномерной сходимости ряда Фурье |