Достаточное условие равномерной сходимости ряда Фурье

Теор. Пусть ф-я f(x) непрерывна на [a;b]; и является кусочно гладкой. Тогда ряд Фурье этой функции равномерно сходится к 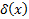на все отрезке [a,b]

Док-во. Так как функция кусочно-гладкая, то она имеет непрерывную на [a,b] производную 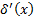всюду, за исключением конечного числа точек {Xi}. Доопределим эту функцию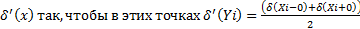

Тогда 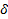’(x) на отрезке [a,b] оказывается принадлежащей классу Q[a,b]и для

Пусть f’(x)соответствует ряд Фурье

А ряд Фурье функции f(x) сходится поточечно к этой функции:

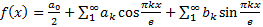
Для доказательства равномерной сходимости используем признак Вейерштрасса, т.е построим сходящийся числовой ряд, который мажорирует Фурье. Найдем связь между коэффициентами a₀,b_k,b_k и ₀, _k, _k

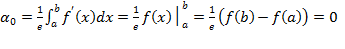
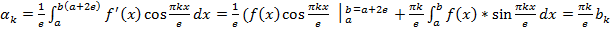
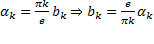
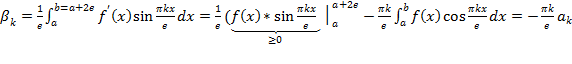
Производим оценку членов ряда

a₀/2=const

f’(x) соответствовал ряд Фурье, а для коэффициентов ряда Фурье справедлива формула

0 эти ряды сходятся

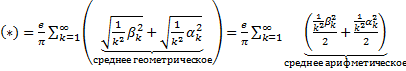Этот ряд сходится => Ряд Фурье для f(x) сходится равномерно

Дата добавления: 2015-10-13