Данное условие необходимо проверять при числе сателлитов пs >2 при равномерном их распределении по окружности.

Условие сборки заключается в определенном взаимном расположении сателлитов и центральных колес. Очевидно, что после установки первого из сателлитов установка последующих оказывается возможной, только если зубья сателлита рас­положены строго напротив впадин сопряженных с этим сателлитом колес. Выполняется это условие при таком подборе чисел зубьев, количестве сателлитов и их взаимного расположения, при которых обеспечивается правильное зацепление во всех парах зубчатых колес. Анали­тически это условие для различных схем записывается как:

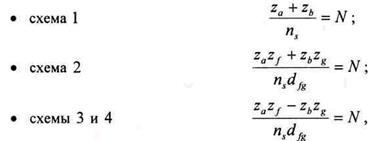
где N - любое целое число (критерий собираемости);

d _fg - наибольший общий делитель чисел зубьев z_f, и z_g.

Если N не равно целому числу, то сборка невозможна. Проверка по условию сборки проводится при числе сателлитов п_s > 1.

Условия правильного зацепления. Выполнение условия правильного зацепления обеспечивает отсутствие заклинивания передачи и достаточно надежную величину коэффициента перекрытия во всех парах зубчатых колес, выполненных без подреза к срезa зубьев.

Во избежание подреза зубьев эвольвентных нулевых колес для переда­чи внешнего зацепления [2] при α = 20° и h_а=1 принимают Z ≥ 17, при h_а=0.8 Z ≥ 14.

Для внутреннего зацепления в [1] приводятся дифференцированные значения допускаемых чисел зубьев (таблица 2.2).

Планетарные механизмы, как правило, проектируются и изготовляются с нулевыми колесами, но их можно составлять и из ненулевых колес с прямыми или косыми зубьями [2]. Число зубьев малого колеса при этом может быть значительно снижено и тем самым уменьшены габариты механизма.

2.3 КПД планетарных передач

При расчете коэффициента полезного действия планетарной передачи можно воспользоваться методом обращенного движения. В качестве примера определим КПД планетарного редуктора, выполненного по схеме 3 с двумя внешними зацеплениями. Рассмотрим вариант, когда энергия передается от центрального колеса к водилу, а неподвижным звеном является колесо b. То­гда согласно определению КПД передачи равен

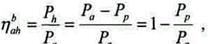(2.10)

где P_a,P_h, и Р_p - соответственно мощности на осях центрального колеса и водила и

мощность потерь в редукторе.

После мысленной остановки водила планетарная передача превращается в простой редуктор с фиксированными осями, так что мож­но записать

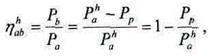(2.11)

откуда

(2.12)

где Р^h_a =T_a │ ω_a – ω_h│; Р_a =T_a │ ω_a │, T_a - вращающий момент на звене а.

Очевидно, что потери мощности не зависят от величин и знака скоростей от­носительного движения. Тогда из (1.10) с помощью (1.11) имеем

(2.13)

Метод расчета, изложенный применительно к одной из возможных кинема­тических схем планетарных редукторов, можно использовать и для определения КПД других схем (см. таблицу 2.1).

2.4 Силовые и энергетические параметры планетарных передач

Рассмотрим силы, действующие на сателлит планетарного редуктора, выполненного по схеме 1, при передаче вращающего момента от входного вала к водилу при неподвижном звене b. Контуры колес и приложенные к ним нагрузки изображены на рис.2.4.

Рис.2.4.

В зацеплении зубьев прямозубых колес сила, нормальная к поверхности зуба, может быть разложе­на на две составляющие - касательную (окружную) к цилиндру колеса F_ta, F_tb и перпендикулярную к ней радиальную F_ra, F_rb. Эти силовые факторы легко определяются из уравнений равновесия. Если момент вращения на входе редуктора обозначить через T_a, то

F_{ta =} T_a / r_a, (2.13)

где r_a - радиус основной окружности центрального колеса.

Так как сателлит вращается с постоянной угловой скоростью, то алгебраи­ческая сумма моментов всех действующих на него сил относительно оси вращения будет равна нулю, следовательно, F_ta = F_rb, а окружное усилие, приложенное к водилу, записывается как

F_th=F_ta+F_tb=2F_ta,. (2.14)

Момент вращения Т_h, водила

T_h = 2F_ta(r_{a +} r_b)/2. (1.15)

где r_b- радиус основной окружности неподвижного звена.

Дата добавления: 2015-09-06