Основные геометрические размеры зубчатых колес

Наименование	Обозначение	Формула
шаг зацепления по делительной окружности	P	P=p*m
радиусы делительных окружностей	r1,2
радиусы основных окружностей
коэффициент суммы смещений	xS	XS= x1+ x2
толщина зуба по делительной окружности	s1,2
угол зацепления	aw	Номограмма (рис.1.1)
Межосевое расстояние	aw
коэффициент воспринимаемого смещения	y
коэффициент уравнительного смещения	Dy	Dy= xS-y
радиусы окружностей впадин
радиусы окружностей вершин
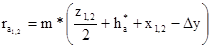
радиусы начальных окружностей
глубина захода зубьев	hd
высота зуба	h	h=ha+c^**m
Проверка 1. rw1+rw2=aw 2. aw-(rf1+ra2)=0,25*m 3. aw-(rf2+ra1)=0,25*m 4. aw-(r1+r2)=y*m	Постоянные ha^*; c^*=0,25; a=20^0 cosa=0,939693 tga=0,363970 p=3,1615926

Коэффициенты смещения х1 и х2 выбираются или из блокирующих контуров или из таблиц профессора В.Н.Кудрявцева (таблицы 1.2., 1.3). Если в таблице 1.3 число зубьев колеса Z2 не кратно 5, то коэффициент смещения Х2 следует брать для ближайшего меньшего значения Z2 кратного 5. Если 2³u1,2³1,, то коэффициенты смещения выбираются по [2].

Таблица 1.2

Значения коэффициента х₁ для неравносмещенного внешнего зацепления

при 5³u_1,2³2

z1
X1	0,66	0,73	0,80	0,80	0,92	0,96	1,04	1,10	1,16	1,22	1,27

Таблица 1.3

Значения коэффициента х₂ для неравносмещенного внешнего зацепления

при 5³u_1,2³2

z2	Значения при z1
	0,442 0,501 0,556 0,610 0,661 0,709 0,754 - - - - - - - - - -	0,442 0,486 0,542 0,596 0,648 0,696 0,745 0,789 - - - - - - - - -	- 0,471 0,528 0,582 0,635 0,685 0,734 0,782 0,822 - - - - - - - -	- 0,463 0,522 0,577 0,632 0,684 0,732 0,780 0,825 0,866 - - - - - - -	- - 0,518 0,575 0,628 0,682 0,731 0,779 0,826 0,870 0,909 - - - - - -	- - 0,512 0,569 0,624 0,677 0,728 0,778 0,827 0,872 0,914 0,954 - - - - -	- - 0,505 0,564 0,620 0,674 0,727 0,777 0,825 0,874 0,917 0,957 0,998 - - - -	- - - 0,560 0,616 0,671 0,722 0,773 0,823 0,871 0,920 0,961 1,001 1,042 - - -	- - - 0,553 0,611 0,667 0,720 0,772 0,821 0,869 0,919 0,962 1,003 1,046 1,086 - -	- - - - 0,606 0,662 0,716 0,769 0,820 0,868 0,916 0,965 1,008 1,048 1,088 1,129 -	- - - - 0,566 0,623 0,677 0,729 0,778 0,828 0,876 0,924 0,964 1,005 1,045 1,087 1,131

Рассмотрим особенности геометрического расчета зубчатых зацеплений.

1) Формулы в таблице 1.1, содержащие индексы 1, 2, заменя­ют собой две формулы. Индекс 1 относится к размерам зубчато­го колеса, имеющего меньшее число зубьев (шестерни), а ин­декс 2 размерам зубчатого колеса, имеющего большее чис­ло зубьев либо (колеса).

2) В курсовых проектах неравносмещенной передачей яв­ляется либо простая зубчатая передача z₄, z₅ привода, либо передача z_a, z_b. Поэтому в таблице 1.1 вместо индексов 1, 2 следует ставить 4, 5 или а, b, а в качестве модуля следует брать модуль для простой передачи m

3) Угол зацепления a_w определяется или по формуле

, (1.4)

где значения inv α и inv α _w определяют с дальнейшим применением таблиц инвалютных углов (см. приложение 2) или по но­мограмме Б.Н.Кудрявцева (см. приложение 1).

Для определения a_w по номограмме (приложение 1) нужно вычислить

в= (1.5)

1.2 Вычерчивание внешнего эвольвентного зацепления

Подсчитав все размеры элементов зацепления по формулам, приведенным в таблице 1.1, приступаем к вычерчиванию зубчатого зацепления.

Масштаб построения выбираем таким образом, чтобы высота зуба на чертеже была не менее 30 мм.

Профили зубьев вычерчивают в такой последовательности (рис.1.1, 1.2):

1) На линии центров колес от точки W (полюса зацепления) откладываем радиусы r_w1 и r_w2 начальных окружнос­тей и строим эти окружности. Для построения больших окружнос­тей удобно пользоваться специальным циркулем;

2) Проводим основные окружности r_b1, r_b2, линию зацепления n-n касательно к основным окружностям и ли­нию t-t, касательно к начальным окружностям через точку их касания W. Под углами a_w к межосевой линии проводим радиусы r_b1 и r_b2 и отмечаем точки А, В тео­ретической линии зацепления;

3) Строим эвольвенты, которые описывает точка W пря­мой АВ при перекатывании ее по основным окружностям. При построении 1-й эвольвенты делим отрезок AW на четыре равные части. На линии зацепления n-n откладываем при­мерно 7 таких равных частей. Также 7 частей откладываем на основной окружности r_b1 от точек А и В, в разные стороны. Из полученных точек на основной окружности проводим радиусы c центром О₁ и перпендикуляры к радиусам. На построенных перпендикулярах (касательных к основной окружности r_b1) откладываем соответственно 1, 2,.... 7 частей, равных расстоянию до W. Соединяя полученные точки плавной кривой получаем эвольвенту для первого колеса. Т.о. строим эвольвенту для второго зубчатого колеса;

4) Строим окружности вершин (головок) r_а1, r_а2 обоих ко­лес;

5) Строим окружности впадин r_f1, r_f2, обоих колес. Следует заметить, что радиус окружности впадин может быть больше, равен и меньше радиуса r_b основной окружности;

6) Из точки пересечения эвольвенты первого колеса с де­лительной окружностью этого колеса r₁, откладываем полови­ну толщины зуба по делительной окружности. Соединив полученную точку с центром O₁ получаем ось симметрии зуба. Симметрично строим другую боковую поверхность зуба. На расстоянии шага по делительной окружности строим еще два зуба. При этом для увеличения точности расположения зубьев шаг Р делим на два и откладываем два раза. Аналогично строим зубья второго колеса;

7) Определяем активную часть линии зацепления. Активной частью линии зацепления называют отрезок ab теоретической линии зацепления, заключенной между точками пересечения ее с окружностями вершин (головок) колес. Активная часть линии зацепления является геометрическим местом точек зацепления (касания) профилей зубьев на неподвижной плоскости;

8) Строим рабочие участки профилей зубьев. Те участки профилей зубьев, которые участвуют в зацеплении называют рабочими. Чтобы найти эти участки через точку а из центра О₁ проводим дугу радиуса О₁а до пересечения с профилем зуба первого колеса. Рабочим участком зуба первого колеса является участок от полученной точки до конца зуба. То же самое производим с зубом второго колеса, проведя окружность О₂b из центра О₂. Чтобы обозначить на чертеже участки, нужно про­вести линии, параллельные эвольвентам на расстоянии 1,5-2 мм и заштриховать получившиеся полоски;

9) Строим дугу зацепления a’b ’ и a”b”. Каждую из дуг начальных окружностей, которые перекрываются одна по дру­гой за время зацепления одной пары сопряженных профилей, на­зывают дугой зацепления. Так как начальные окружности r_w перекатываются друг по другу без скольжения, те дуги зацепления обоих колес равны между собой;

10) Для построения дуги зацепления первого колеса, через крайние точки рабочего участка профиля зуба В₁С₁ проводим нормали к этому профиле (они являются касательными к основной окружности r_b1 первого колеса). Находим точки пересечения этих нормалей с начальной окружностью r_w1 первого колеса. Полученные точки ограничивает дугу зацепления первого колеса. Аналогично поступаем со вторым колесом.

1.3 Определение качественных показателей зацепления

Качественными показателями зацепления являются коэффици­енты перекрытия e_a, относительно скольжения n и удель­ного давления.

1) Коэффициентом перекрытия e_a называют отношение дли­ны дуги зацепления к длине шага по начальным окружностям.

Аналитический коэффициент перекрытия можно найти из формулы:

(1.6)

После строения картины зацепления (совмещенный рис.1.1,1.2) можно найти графический коэффициент перекрытия по формуле:

, (1.7)

где ab - длина активного участка линии зацепления, взя­тая с учетом масштаба.

После нахождения аналитического и графического коэффи­циентов перекрытия находим процент их расхождения.

. (1.8)

2) Определяем коэффициент относительного скольжения. Так как рабочие участки профилей зубьев перекрываются друг по другу со скольжением, то на этих участках возникают силы трения и происходит процесс изнашивания. Характеристикой вредного влияния скольжения являются коэффициенты n₁ и n₂ относительного скольжения, которые определяют по формулам:

, (1.9)

где i=AB - длина теоретической линии зацепления;

х - расстояние от точки А касания теоретической линии зацепления с

основной окружностью первого (меньшего) колеса, отсчитываемое в

направлении к точке В (рис.1.2);

,

(1.10)

Пользуясь формулами (1.8), составляем таблицу 1.4 значений n₁ и n₂. Для этого измеряем длину i на рис. 1.2, под­ставляем полученное значение в формулы (1.7), а затем подсчиты­ваем ряд значении n₁ и n₂ изменяя Х в границах от 0 до l с интервалами 15 - 30 мм.

Необходимо знать, что в полюсе зацепления W коэффициенты скольжения равны нулю.

Таблица 1.4

Значения коэффициентов скольжения.

x		...	AW	...	l
n1
n2

По таблице 1.4 строим диаграмму для значений коэффициентов n₁ и n₂ в прямоугольной системе координат рис.1.2. Далее строим круговые диаграммы. Круговые диаграммы – называются диаграммы коэффициентов n₁ и n₂ на активных участках сопряженных профилей зубьев. Для построения круговой диаграммы первого колеса значение х проецируем на активную часть ab линии зацепления. Из полученной точки проводим окружность с центром О ₁. На этой окружности откладываем значение коэффициента скольжения n_{1 .} При этом положительные значения n₁, откладываем в наружную сторону от зуба, а отрицательные - во внутреннюю сторону. Аналогично поступаем с коэффициентом скольжения n₂.

Рис.1.1 Схема зацепления

Рис.1.2 Определение качественных показателей зацепления

2. СИНТЕЗ ПЛАНЕТАРНЫХ И ДИФФЕРЕНЦИАЛЬНЫХ ПЕРЕДАЧ

Геометрические оси колес в рассмотренных ранее видах зубчатых передач неподвижны. Однако в практике проектирования передаточных механизмов часто используются передачи, хотя бы одна ось которых перемещается. Эти передачи называются планетарными. Если же подвижными являются все оси, то передача называется дифференциальной. Планетарные и дифференциальные передачи име­ют широкие кинематические возможности. Они более компактны и имеют мень­ший вес по сравнению с остальными зубчатыми, что позволяет применять плане­тарные передачи в летательных аппаратах, аппаратах электронной техники и на других объектах, для которых существенна экономия места и веса. И планетарные, и дифференциальные передачи представляют класс передаточных механизмов, широко распространенный при проектировании машин, и в этой связи на их описа­нии следует остановиться подробнее

Следует отметить, что методы расчета прочности зуб­чатых передач с неподвижными осями, которые рассматриваются в деталях машин, можно полностью перенести на процесс проектирования планетарных и дифференциальных, но существует ряд особенно­стей, характерных именно для этого типа передаточных механизмов. Рассмотрим сначала эти особенности применительно к планетарным передачам, а затем ука­жем, как от планетарных перейти к дифференциальным.

При проектировании планетарного механизма по выбранной схеме и заданному передаточному отношению желательно с минимальным объемом вычислений подобрать числа зубьев колес, при которых получились бы наименьшие размеры механизма. При прочих равных условиях наименьшие габариты механизма получаются при выборе минимально возможных чисел зубьев колес.

Выбранные числа зубьев колес планетарного механизма должны удовлетворять следующим основным условиям:

- обеспечение заданного передаточного отношения;

- соосность центральных зубчатых колес;

- возможность сборки механизма;

- соседство смежных сателлитов;

- правильное зацепление каждой пары зубчатых колес.

От того, насколько удачно подобраны числа зубьев зубчатых колес будут зависеть такие качественные характеристики проектируемого механиз­ма, как компактность, масса, технологичность и др.

Основные кинематические схемы планетарных передач. Конструктивно планетарные передачи состоят из зубчатых колес с подвижными осями - сателли­тов. Оси сателлитов закреплены на водиле (на схемах обозначается как h). Зубча­тые колеса, по которым обкатываются сателлиты, носят название центральных. Неподвижное центральное колесо называется опорным. Можно сконструировать большое количество разнообразных схем планетарных передач с различными си­ловыми, энергетическими, кинематическими и другими характеристиками, но в практике проектирования используют довольно ограниченный набор планетарных механизмов. Ниже (рис.2.1) приведены кинематические схемы наиболее распро­страненных планетарных передач, на примере которых мы рассмотрим общие ме­тоды их проектирования.

Рис.2.1 Основные типы планетарных механизмов

схема 1 - с одним внутренним зацеплением;

схема 2 - с внутренним и с внешним зацеплениями;

схема 3 - с двумя внешними зацеплениями;

схема 4- с двумя внутренними зацеплениями.

На схемах (рис.2.1) обозначено:

a u b - центральные зубчатые колеса;

f u g - промежуточные зубчатые колеса - сателлиты;

h - опора промежуточных зубчатых колес (водило).

Элементы кинематических пар, принадлежащие неподвижному звену (стойке) подштрихованы.

Приведенные на рис.2.1 механизмы могут обеспечить как понижение числа оборотов от ведущего звена к ведомому (редукторы), так и повышение числа оборотов (мультипликаторы). Однако, вследствие возможного самоторможения или получения механизма с низким КПД планетарные механизмы в качестве мультипликаторов обычно не применяют.

Для планетарных передач важным конструктивным фактором является ус­ловие закрепления их звеньев. Одна и та же кинематическая схема планетарного редуктора может иметь абсолютно различные характеристики в зависимости от того, которое из его звеньев является неподвижным. Например, из представленных на рис.2.1 схем наиболее распространенной является схема 1, причем при усло­вии, что ведущим звеном служит колесо а, а неподвижным - b. Эта схема приме­няется для передач с передаточным отношением и≤ 8 и имеет высокий КПД. Ко­гда же ведущим звеном становится колесо b, то значения передаточного отноше­ния уменьшаются в 2 - 4,5 раза (см. таблицу 2.1), но при таком конструктивном ре­шении данная кинематическая схема применяется редко.

Если необходимо обеспечить передаточ­ное отношение еще большее, чем в схеме 1 с ведущим звеном а, то можно последовательно установить несколько таких передач (рис.2.2), тогда, передаточное отношение кинематической цепи будет равным произведе­нию передаточных отношений ее элементов. Для передачи, выполненной по схеме 2, можно полу­чить и <= 16, при этом ее размеры будут несколь­ко меньше, чем для передачи по схеме 1, но и КПД тоже ниже.

Очень большие передаточные отношения можно получить, если в качестве ведущего звена использовать водило. Правда, такие схемы пере­дач имеют значительно более низкий КПД.

Рис.2.2

Схемы 3 и 4 применяются существенно реже схем 1 и 2, и только для малых нагрузок, так как они имеют низкий КПД.

Рассмотрим кратко условия, которые необходимо выполнять при синтезе планетарных зубчатых механизмов.

2.1 Передаточное отношение планетарных передач

Наиболее простым и вме­сте с тем распространенным методом расчета передаточного отношения планетар­ных передач является метод обращенного движения, при котором водило мыслен­но останавливается, а планетарный редуктор преобразуется в редуктор с фиксиро­ванными (неподвижными) осями. Продемонстрируем этот метод на примере передачи, выполненной по схеме 1 с неподвижным ведомым звеном b.

Для остановки водила необходимо сообщить ему дополнительную угловую

скорость, равную — ω^b_h. В результате такой остановки остальные звенья, участ­вующие в движении - колеса я и 6 - приобретают угловые скорости ω^h_a и ω^h_b:

ω^h_{a =} ω^b_a – ω^b_h; ω^h_{b =} – ω^b_h, (2.1)

где ω^b_a - угловая скорость колеса а до остановки водила.

Передаточное отноше­ние и^b_ah редуктора, по определению, равно

и^b_{ah =} ω^b_a / ω^b_h, (2.2)

поскольку при ведущем колесе а и ведомом b выходным звеном служит водило, Здесь и далее верхний индекс обозначает неподвижное звено, первая буква нижне­го индекса - ведущее, а вторая - ведомое звенья.

Передаточное отношение и^h_ab колес с учетом (2.2) имеет вид:

(2.3)

Так как передаточное отношение и^h_ab определяется по обычной для зубчатых редукторов методике, то и^h_ab= - z_b / z_a, где z_b, z_a - числа зубьев колеса и а и b, что при подстановке в (2.3) дает

(2.4)

Описанный метод расчета передаточного отношения остановкой водила можно успешно использовать для опpeдeлeния передаточных чисел всего многооб­разия конструкций планетарных передач. В частности, для схемы 2 в случае, если звено b неподвижно, а числа зубьев звеньев g и f равны соответственно z_g и z_f, имеем

(2.5)

Значения передаточных отношений и других параметров планетарных передач основных кинематических схем приведены в таблице 2.1.

2.2 Подбор чисел зубьев планетарных передач

В силу конструктивных особенностей планетарных передач их расчет проводится при соблюдении ряда до­полнительных ограничений. Так, если при проектировании обычных зубчатых пе­редач достаточно обеспечить удовлетворительное значение коэффициента пере­крытия, отсутствие подреза и заострения зуба, а также отсутствие интерференции, то для планетарных передач этот список ограничений расширяется. В процессе конструирования планетарных передач должны быть выполнены следующие спе­циальные условия:

• соосности;

• соседства;

• сборки.

Таблица 1.1

Кинематические параметры типовых планетарных передач

Условие соосности предусматривает равенство межосевых расстояний раз­личных пар зубчатых колес передачи, что может быть обеспечено выбором соот­ветствующего числа зубьев и наличием смещения инструмента. Это условие при­менительно к схеме 1 имеет вид

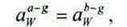(2.6)

для схем 2—4

(2.7)

Условие соосности будет выполнено, если подобрать числа зубьев звеньев таким образом, что при нарезании колес без смещения выполняются следующие соотношения:

Здесь m₁ и m₂, - модули зубьев пар a—g и b—f соответственно.

Условие соседства требует отсутствия задевания головок зубьев соседних (рядом расположенных) сателлитов, т.е. проверяет наличие зазора между сателлитами в передаче (рис.1.3). Для того чтобы обес­печить такой зазор, необходимо выполнение следующего неравенства:

(2.8)

где β = π / п_s, - угол между осями сателлитов;

п_s и d_as - число сателлитов и их внешний диаметр;

ОА = a_w - межосевое расстояние.

Рис.1.3 Условие соседства

Дата добавления: 2015-09-06