Радиальные со­ставляющие в полюсах зацепления имеют вид

(2.16)

где α - угол зацепления в зубчатой паре.

Реактивный момент T_b, воспринимае­мый крепежными элементами звена b, равен

(2.17)

Силы в зацеплении зубьев можно определить другим способом, если вос­пользоваться уравнением равновесия моментов вращения, а именно

(2.18)

Можно обратиться также к уравнению закона сохранения энергии, которое применительно к рассматриваемому случаю имеет вид

(2.19)

Обычно один из моментов T_a,T_b и T_h является известным, а остальные можно определить совместным решением уравнений (2.18) и (2.19). По извест­ным величинам моментов легко находятся окружные составляющие нагрузки и, как следствие, радиальные составляющие нагрузок в контакте.

Определим усилия в плане­тарном редукторе с двумя внеш­ними зацеплениями (схема 3, рис.2.5). Из уравнения равновесия имеем F_ta r_g=F_tb r_f,, или

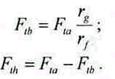(2.20)

Рис.2.5. Рис.2.6.

Для случая редуктора с од­ним внешним и одним внутренними зацеплениями (схема 2, рис.2.6) имеем

F_ta r_g=F_tb r_f; F_tb = F_ta r_g /r_f; F_th =F_ta + F_tb. (2.21)

Аналогично определяются силы в зацеплениях для других схем планетарных передач.

2.5 Особенности прочностного расчета планетарной передачи

Проектиро­вочный расчет планетарных передач в основном не отличается от расчета обычной передачи, за некоторым исключением. Дело в том, что в планетарной передаче момент вращения передается по нескольким потокам, и из-за наличия погрешностей изготовления и монтажа моменты, передаваемые каждым из потоков, оказываются различными. Это явление можно охарактеризовать введением коэффициента неравномерности нагрузки по потокам К_р. Значение коэффи­циента неравномерности зависит от точности изготовления элементов передачи, их деформаций и ряда других факторов. Полученные при этом аналитические реше­ния, основанные на анализе простых моделей, малодостоверны и могут быть опре­делены только с помощью проверочного расчета. При проектировании новых кон­струкций для выбора коэффициента неравномерности нагрузки по потокам можно воспользоваться эмпирическими рекомендациями, принимая его равным К_р=1,35-1,5.

Для снижения неравномерности нагрузки по потокам иногда применяют та­кую конструкцию, при которой центральное колесо выполняется плавающим, без использования жестких опор. Тогда К_р = 1,10 -1,15.

При определении числа циклов нагружения зубчатых колес необходимо помнить, что преобразование планетарного редуктора в редуктор с неподвижными осями достигается остановкой водила, так что угловые скорости всех участвую­щих в кинематической цепи колес уменьшаются на величину угловой скорости водила.

Дифференциальная передача. Дифференциальная передача получается из планетарной, если освободить центральное опорное колесо. Образованный таким образом передаточный механизм с дополнительной степенью свободы позволяет суммировать два движения или, напротив, разделять одно на два. На практике дифференциальные передачи в основном используют для преобразования движе­ния от двигателя на два ведомых вала, реже - когда движение от двух двигателей передается на один ведомый вал. Дифференциальные механизмы можно встретить и в совокупности с обычными передачами.

В качестве примера дифференциальной передачи рассмотрим механизм, выполненный по схеме 1, но не имеющий закрепленных звеньев. В обращенном движении имеем следующее передаточное отношение и_ab редуктора в относи­тельном движении:

(2.22)

Разрешая (2.22), относительно угловой скорости ω_b, получаем

(2.23)

Выражение (2.23) можно переписать через углы поворота звеньев:

(2.24)

Согласно (1.24), зная законы изменения углов поворота каждого из двух независимых звеньев, можно получить закон изменения угла поворота третьего звена.

Если и_ab =2, то φ_b=[φ_a+φ_h]/2, а полученный дифференциальный меха­низм позволяет суммировать два независимых движения. Результат такого сумми­рования определится как среднее арифметическое от составляющих движений.

В качестве другого примера можно рассмотреть конструкцию конического дифферен­циала (рис. 2.7), который поворотом водила на угол, рассчитанный по формуле (2.24), сумми­рует два независимых движения конических шестерен. Такой механизм также называют сумми­рующим, так как результирующий угол поворота равен сумме сигналов, умноженных на постоянные коэффициенты, зависящие от геометрии механизма.

Методика прочностного и силового расчета дифференциальных механизмов та же, что и для простых планетарных передач.

Рис.2.7. Дифференциал.

ЛИТЕРАТУРА

1. Артоболевский И.И. Теория механизмов и машин. - М.: Наука, 1975. - 639 с.

2. Кореняко А.С. и др. Курсовое проектирование по теории механизмов и машин. - Киев: Высшая школа, 1970. – ЗЗ6 с.

3. Фролов К.Е. Теория механизмов и машин. - М.: Высшая школа, 1967. - 493 с.

4. Попов С.А. Курсовое проектирование по теории механиз­мов и машин. -И.: Высшая школа, 1936. - 291 с.

Дата добавления: 2015-09-06