Геометрические параметры эвольвентного зацепления.

Цилиндрические прямозубые передачи

(П .Г Гузенков «Детали машин» §§12.2, 12.3

М.Н. Иванов «Детали машин» §8.2)

Во время передачи движения зацеплением зубьев важно выполнить ряд условий, предъявляемых к ним при производстве и эксплуатации передач.

1. Кинематическое условие – U = const

Профили зубьев передачи должны обеспечивать постоянство передаточного числа – U.

2. Энергетическое условие.

Для обеспечения высокого К.П.Д., прочности и долговечности колес, профили должны обеспечивать малые скорости скольжения – Vск и достаточные радиусы кривизны в пятнах контакта зубьев.

3. Технологическое условие (производственное).

Профили зубьев должны удовлетворять условию легкого изготовления, в частности нарезанию простым инструментом, независимо от числа зубьев колес.

Этим требованиям наиболее полно удовлетворяет эвольвентное зацепление.

Оно разработано Л. Эйлером в 1760 г. и нашло широкое применение в машиностроении.

Зубчатое колесо эвольвентного профиля может входить в зацепление с другими колесами того же профиля, независимо от числа зубьев колес, нарезается простым инструментом, имеющим прямолинейный профиль зубьев, удобно для контроля. Зацепление малочувствительно к отклонениям межосевого расстояния, допускает корригирование.

Геометричкские параметры зубчатого зацепления (Рис. 1.)

О₁ – О₂ – оси зубчатых колес.

а_W – межосевое расстояние.

Передаточное число зубчатой передачи определяется отношением радиусов О₂Р и О₁ Р.

,

где р – полюс зацепления.

Радиусы О₂Р и О₁ Р принадлежат окружностям, которыми перекатываются друг по другу без скольжения начальные окружности d _W1 и d_W2.

Во время передачи движения зуб ведущего зубчатого колеса входит в контакт, т.е. в зацепление с зубом ведомого колеса. При относительном перекатывании зубьев точка их контакта перемешается по некоторой наклонной линии, проходящей через полюс зацепления.

Геометрическое место точек контакта зубьев сопряженных профилей, называется линией зацепления.

В пространстве линия зацепления расположена по нормали к поверхности пятна контакта сопряженных поверхностей зубьев.

Рис. 1.

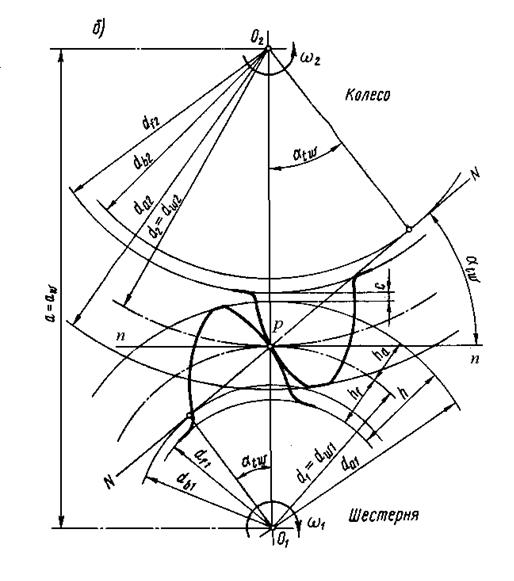
Линия зацепления наклонена к нормали n – n, проходящей через полюс, под углом a _W, где a _W – угол зацепления по ГОСТ 13755 – 81.

Эвольвентные профили зубьев образованы траекторией движения точки М, расположенной на прямой N – N обкатываемой без скольжения по окружностям с центрами О₁ и О₂, соответственно называемыми основными окружностями d _В1 и d _В2.

d _В = d_W·cos a _W.

Диаметр окружности предназначенной для определения элементов зубьев и их размеров называется делительным – d.

d – диаметр делительной окружности.

Поверхность, отделяющая зубья от тела зубчатого колеса называется поверхностью впадин.

d f – диаметр окружностей впадин.

Поверхность, проходящая по вершинам зубьев зубчатого колеса, называется поверхностью вершин зубьев.

d α – диаметр окружностей вершин зубьев.

Расстояние между одноименными поверхностями соседних зубьев, измеренное по дуге концентрической окружности зубчатого колеса, называется окружным шагом – р_t.

Различают делительный, начальный и другие окружные шаги зубьев.

Для косых шевронных и криволинейных зубьев кроме окружного шага различают шаг измеренный в плоскости перпендикулярной оси симметрии зуба – нормальный шаг – р_n.

р_n = р_t·cos β

где β – угол наклона зубьев по делительному диаметру; β = 8 …40⁰.

Линейная величина в π раз меньшая окружности шага зубьев, называется модулем зубьев – m

m_t = 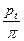– окружной модуль;

m_n = 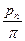– нормальный модуль.

m_n = m_t · cos β – для косых зубьев;

m_n = m_t – для прямых зубьев.

Модуль – m основная характеристика размеров зубчатых и червячных колес.

Модули эвольвентных зубчатых колес стандартизованы по ГОСТ 9563 – 60.

Стандарты распространяются на цилиндрические и конические зубчатые колеса с прямыми зубьями. Они устанавливают, для цилиндрических колес значения нормальных модулей, для конических – значения внешних окружных делительных модулей.

Стандартом ГОСТ9563-60 предусмотрено два ряда модулей m (первый ряд считается предпочтительным), мм:

1-й ряд: …; 1,0; 1,25; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40; … 100.

2-й ряд: …; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22; 28; 36; 45; … 90.

При бесконечно большом числе зубчатого колеса, оно превращается в рейку, а эвольвентный профиль зуба – в прямолинейный, удобный для изготовления и измерения.

Контур профиля зубьев, полученный при Ζ ® ∞ называется исходным контуром.

В соответствии с исходным контуром осуществляется профилирование зубьев

эвольвентного зацепления и инструмента для их нарезания.

Параметры нормального сечения зубчатых колес с модулем m ³ 1 выбираются по ГОСТ 13755-81 (Рис. 2).

Для конических зубчатых колес с прямыми зубьями ГОСТ13754 – 68.

α – угол профиля зуба, α = 20⁰;

а – а – средняя линия;

р – шаг;

h_a – высота головки зуба, h_a = m;

h_f – высота ножки зуба, h_f = 1,25m;

c – радиальный зазор, с = 0,25m;

h_W – высота зуба, h_W = 2,25 m.

Диаметр делительной окружности – d

πd = p·Z = π·m·Z, где Z – число зубьев

d = m·Z

Диаметр окружности вершин зубьев

d_a = d + 2 m = m Z + 2m = m(Z + 2).

Диаметр окружности впадин

d_f = d + 2,5 m.

Коэффициент ширины зубьев – y выбирают по ГОСТ 2185 – 55

y_ba = 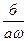; y_bd = ; y_bm = .

Ширина зубчатого колеса – б определяется из вышеприведенных формул:

Межосевое расстояние – а_W рассчитывают по формуле

а_W = .

---

Дата добавления: 2015-09-05