Определение двойного интеграла. Критерий интегрируемости. Интегрируемость непрерывных в ограниченной замкнутой области функций.

Критерий интегрируемости

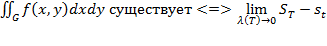
Теор: Пусть f(xy) непрерывна в замкнутой области G. Тогда f(xy) интегрируема в G.(Замкнутая область G содержит свою границу dG)

Док-во

По теореме Кантора f(xy) равномерно непрерывна в G

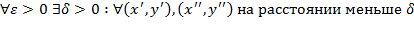
Т такое, что <

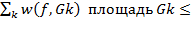
площадь G

По крит интегр f(xy) инт в G

2. Свойства двойного интеграла.

1. Если f(x,y) интегрируема в G, то она останется интегрируемой и интеграл не изменится, если f(x,y) изменить (оставив ограниченной) на кривую (нулевой площади)

2. Аддитивность. f(x,y) интегрируема в G. G разбита кривой Г на G₁ и G_2.­Тогда f интегрируема на G₁ и G₂

3. Линейность. f и g интегрируемы в G. интегрируемы в G

4. Произведение интегрируемых функций интегрируемо

5. Если f(x,y) и g(x,y) интегрируемы в G и f(x,y) g(x,y) в G, то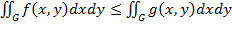

6. Модуль интегрируемой функции интегрируем.

7. Теорема о среднем значении. f(x,y) интегрируема в G. M=sup_G f(x,y), m=inf_Gf(x,y) . Если f(x,y) непрерывна в G, то

8. Площадь G=

3. Сведение двойного интеграла к повторному. Случай прямоугольной области

Теор. f(x,y) интегрируема в R { }

.

Тогда: а) I(x) интегрируема на [ab]

б)

Дата добавления: 2015-10-13