Дайте определение уровню равной громкости.

ривые равной громкости (см. рис. А-6) показывают, какая требуется разница в уровне звукового давления, чтобы звуки всех частот воспринимались с такой же громкостью, как референсный синусоидальный сигнал с частотой 1 кГц. Числа, находящиеся над каждой кривой, представляют собой меру громкости, выраженную в фонах. На референсной частоте 1 кГц фоны равны децибелам.

Выгодные предложения бытовая техника одесса огромный выбор.

К примеру, при очень низком уровне громкости 30 фон (30 дБ SPL на частоте 1 кГц) басовый тон 50 Гц должен воспроизводиться с уровнем 60 дБ SPL, чтобы он воспринимался с такой же громкостью, как звук 30 дБ SPL с частотой 1 кГц. Иными словами, наши уши менее чувствительны в области низких и высоких частот, нежели на средних частотах.

Вечернее платье в Инта.

Эта существенная неравномерность чувствительности по частоте наиболее велика при низких уровнях звукового давления, что проявляется в значительной неравномерности кривых в нижней части графика и постепенным выравниванием их в верхней части. По мере возрастания SPL человеческие уши становятся примерно одинаково восприимчивы ко всем частотам. При громкости ПО фон (ПО дБ, частота 1 кГц), звук с частотой 50 Гц должен воспроизводиться на уровне 120 дБ, чтобы он воспринимался равным по громкости звуку с частотой 1 кГц — довольно заметная разница с приведенным выше примером (30 фон).

Балка двутавровая демонтажная в короткие сроки.

Этот эффект знаком всем. Поворачивая регулятор усиления своей Hi-fi-системы в сторону увеличения громкости, вы начинаете лучше различать басы и верхние частоты. Кажется, что басы захватывают более широкий диапазон частот. Напротив, если снизить громкость до такого уровня, когда звук едва слышен, то различаются только средние частоты. Кнопка "тонкомпенсация" ("Loudness") в аппаратуре среднего класса усиливает басы и верхние частоты, чтобы компенсировать пониженную восприимчивость уха к ним при малой громкости звука.

По разделу «Операции с дБ» - лекция 4

Можно ли уровни складывать как обычные числа?

Уровни звукового давления нельзя складывать и вычитать как обычные числа. Для определения суммарного уровня звукового давления (далее УЗД) от нескольких источников шума в одной точке нужно учитывать их логарифмическую зависимость. Для сложения необходимо от УЗД перейти к абсолютным значениям интенсивности звука. Затем, просуммировав их, выполнить обратный переход к суммарному уровню интенсивности звука.

Как определяют сумму двух уровней звукового давления?

В этом тексте ответы ко всему разделу 4

децибел не является физической величиной.
Децибел − это десятичный логарифм, т.е. величина чисто математическая, подчиняющаяся математическим (см. Раздел 2), а не физическим законам.
Поэтому при совместном действии двух и более источников звука (шума) результи­рующий уровень интенсивности (силы) звука не может быть выражен простым сложением их физических характеристик. Необходимо находить логарифмы суммы их интенсивности или квадратов их звуковых давлений, пользуясь формулой (30):

По данным Герхарда Молля, приведем несколько своеобразных при­меров такого сложения:

1 дБ + 1 дБ = 3 дБ
70 дБ + 70 дБ = 73 дБ
50 дБ + 50 дБ + 50 дБ + 50 дБ = 56 дБ
Историческая справка
Gerhard Moll, (1785—1838) — проф. физики и HматематикиH, HдиректорH обсерватории в Утрехте. Работы его относятся преимущественно к электромагнетизму. Чаще цитируется его HисследованиеH, произведенное им в 1823 г. вместе с Van Beck над скоростью звука. Полученный ими результат для скорости звука в сухом воздухе при 0° — 332,25 м/c — считается одним из наиболее точных.

Эти примеры, хотя и очень наглядные, по форме записи не вполне правильные. Правильно записать их в виде формулы (31), имеющей большое практическое значение:

где,
Li − уровни звукового давления источников шума
n − количество источников шума

Эти примеры, хотя и очень наглядные, по форме записи не вполне правильные. Правильно записать их в виде формулы (31), имеющей большое практическое значение:

где,
Li − уровни звукового давления источников шума
n − количество источников шума

Рассмотрим эту формулу более подробно применительно к результирующему уровню интенсивности звука двух источников звука, одновременно работающих c одинаковой интенсивностью (бел).
Для решения этой задачи введём некоторые обозначения:

L1 − уровень интенсивности звука первого источника звука (дБ).
L2 − уровень интенсивности звука второго источника звука (дБ).
Lрез − искомый результирующий уровень звука (дБ).
L1 = L2 = 10 (дБ) − основное условие задачи (дБ).
Руководствуясь формулой (31) мы вправе записать и решить логарифмическое уравнение:

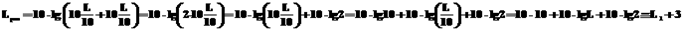
Увеличение в два раза количества источников звука, имеющих одинаковый уровень звука,
приводит к повышению общего уровня интенсивности (силы) звука только на 3 дБ.
Это утверждение справедливо для любого уровня интенсивности звука.

Из этого утверждения и формулы (31) следует, что при n одинаковых источниках шума с уровнями Li результирующий уровень шума в децибелах (дБ) равен (формула 32):

Lрез = Li + 10•lgn (32)
U Примеры

· При

n = 4 и Li = 50 дБ
Lрез = Li + 10•lgn = 50 + 10•lg4 ≈ 50 + 10•6 = 56 дБ

· При одновременной работе четырех мотоцик­летных двигателей, уровень звукового давления каждого из которых составляет 80 дБ, результирующий уровень составит 86 дБ. После отъезда двух мотоциклов результирующий уровень звукового давления снизится всего на 3 дБ и составит 83 дБ.

Весьма интересным и, на первый взгляд, противоречивым является тот факт, что два одинаково громких источника звука при их совместном действии на слух ощущаются не так громко, как удвоен­ный по громкости одиночный источник звука.
Попробуем это объяснить, исходя из приведённых выше формул.
Мы определили, что при удвоении количества источников звука, работающих с одинаковой интенсивностью, результирующий уровень интенсивности увеличится только на 3 децибела (дБ).
Допустим у нас есть источник звука, работающий с уровнем интенсивности равным L1 (дБ).
Вопрос:
Как измениться уровень интенсивности звука этого источника (дБ), если увеличить интенсивность его звучания, например, в два раза.
Сокращённо условия задачи можно записать следующим образом:

I1 − первоначальная интенсивность источника звука.
P1− первоначальное звуковое давление.
I2 − изменённая интенсивность источника звука.
P2 − звуковое давление после изменения.
L1 − первоначальный уровень интенсивности звука источника звука (дБ).
L2 − изменённый уровень интенсивности звука источника звука (дБ).
I2 = 2I1− основное условие задачи

Поскольку мы имеем один источник звука воспользуемся пропорциональностью (21) и формулой (30), запишем:

U Ответ: U Уровень интенсивности звука при удвоении его интенсивности увеличивается на 12 дБ

Дата добавления: 2015-09-05