Уравнение провисания несущего троса цепных подвесок

Общие понятия. Основной частью расчета цепной подвески явля­ется расчет натяжений и стрел провеса несущего троса. Особенность этого расчета заключается в том, что несущий трос цепной подвески, кроме нагрузки от собственного веса и дополнительных нагрузок от гололеда и ветра, воспринимает также нагрузки от подвешенных к не­му контактных и вспомогательных проводов, включая и дополнитель­ные нагрузки от гололеда, а в некоторых случаях и ветра на эти про­вода. Значение нагрузки, передающейся с контактного проводя на несущий трос, зависит от стрел провеса и натяжений вспомогатель­ного и контактного проводов.

Рассмотрим схемы нагрузок, действующих на контактный провод при различном его расположении в вертикальной плоскости (рис. 83). Как видно на рис. 83, а, на контактный провод действуют равномер­но распределенная нагрузка g_K от веса провода и равномерно распре­деленная нагрузка g'_K, обусловленная натяжением контактного про­вода.

Нагрузку g’_K в пролете / при натяжении контактного провода К и

стреле его провеса f нетрудно найти из соотношения от-

куда имеем

В случае положительной стрелы провеса контактного провода (+f) нагрузка g'_K будет положительной и направленной вверх (см. рис. 83, а). На несущий трос с контактного провода в этом случае бу­дет передаваться равномерно распределенная нагрузка

При определенной положительной стреле провеса контактного провода нагрузка g'_K может оказаться равной g_K. В этом случае g_m= 0, так как контактный провод под действием его натяжения К ока­зался полностью самонесущим: на несущий трос через струны не передается никакая нагрузка от веса контактного провода.

Например, контактный провод МФ-100, имеющий натяжение К= 10 кН, будет полностью самонесущим (g’_K = g_K — 0,89 даН/м) в пролете 60 м, когда его стрела провеса

-121-

В случае такой стрелы провеса контактного провода вес его будет вое приниматься опорными струнами и передаваться через них на поддер­живающие устройствам все другие струны в пролете, разгружены.

В компенсированный цепных подвесках контактный провод мон­тируют со стрелой провеса, равной примерно 0,001 /, т. е. при 1_К= 60 м стрела провеса контактного провода даже при наивысшей температуре окружающего воздуха меньше, чем у свободно подве­шенного контактного провода в пролете /. Поэтому в цепных под­весках монтактный провод несет сам только часть нагрузки от собст­венного веса, действующего на него, другая часть g_кт через струны передается на несущий трос.

Подставляя в формулу (34) значения g’_к из выражения (33), получим

При беспровесном положении контактного провода (рис. 83, б) / = 0, следовательно, g’_к =-0. Контактный провод в этом случае сам не несет никакой нагрузки, последняя полностью передается на несу­щий трос: g_кт = g_к .

При отрицательных стрелах провеса контактного провода (рис. 83, а), которые могут быть в полукомпенсированных подвесках, g_’к будет иметь отрицательное значение (направлена вниз). В этом слу­чае согласно формуле (34)

т. е. несущий трос будет нести не только нагрузку g_к от веса контакт­ного провода и действующих на него дополнительных нагрузок, но также и нагрузку g’_к, обусловленную натяжением контактного про­вода.

Нагрузку g'_K контактный провод в виде сосредоточенных сил пере­дает через крайние струны его пролета на поддерживающие устрой-

-122-

ства (консоли) при /_к = / (рис. 84, а) или непосредственно на несущий трос, когда длина части пролета /_к , в которой кон­тактный провод имеет провес, меньше длины пролета несущего троса (рис. 84, б).

Сосредоточенная сила при 1_к=1

Выведем уравнения провисания несущего троса цепной подвески для некоторых схем нагрузок, передающихся на несущий трос с кон­тактного провода. Состояние равновесия цепной подвески будем рас­сматривать в вертикальной плоскости.

Для вывода уравнений провисания несущего троса цепных подве­сок различных конструкций примем следующие обозначения:

-123-

Наиболее простой расчетной схемой является схема, при которой с контактного провода на несущий трос (через большое количество струн) передается равномерно распределенная по всему пролету верти­кальная нагрузка. В действительности же с контактного провода на несущий трос передаются через несколько струн вертикальные сосре­доточенные нагрузки, а в рессорных подвесках — еще и горизонталь­ные от натяжения проводов рессорных струн. Расчетную схему выби­рают в зависимости от конструкции и параметров цепной подвески, а также от точности, с которой должны быть рассчитаны провесы несу­щего троса подвески в различных точках пролета.

Уравнение провисания несущего троса цепной подвески при равно­мерно распределенной нагрузке. Для вывода уравнения провисания несущего троса цепной подвески при передающейся с контактного про­вода на несущий трос (большим количеством струн) равномерно рас­пределенной по всему пролету вертикальной нагрузки воспользуем­ся схемами, показанными на рис. 85.

-124-

В таком виде они хорошо показывают влияние натяжения контакт­ного провода при различных стрелах его провеса на стрелу провеса и натяжение некомпенсированного несущего троса. При положительных значениях f натяжение некомпенсированного несущего троса меньше, а при отрицательных — больше его натяжения Т₀ при беспровесном положении контактного провода.

Приняв в выражениях (42) и (43) / = 0, получим:

Нетрудно видеть, что величина, стоящая в скобках, играет роль эквивалентной переменной (зависящей от F — F₀) нагрузки. Следова­тельно, расчет несущего троса цепной подвески есть тот же расчет свободного подвешивания провода (гибкой нити), но с переменной нагрузкой:

-125-

Подставив значения F и F₉ соответственно из выражений (42) и (44)в (46), получим

и после соответствующих преобразований

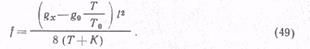
Если в уравнение (42) вместо f подставить его значение из (49), то •после соответствующих преобразований имеем:

Рассматривая эти выражения, видим, что для определения F (компенсированной и полукомпенсированной подвесок) и Т (полукомпенсированной подвески) необходимо знать Т₀, т. е. номинальное (на­чальное) натяжение несущего троса компенсированной подвески или соответственно натяжение несущего троса полукомпенсированной под­вески при беспровесном положении контактных проводов.

Выше были приведены формулы для расчета провисания несущего троса цепной подвески при передающейся с контактного провода на не­сущий трос равномерно распределенной вертикальной нагрузки через большое количество струн в пролете. Обычно же в цепных подвесках, особенно с одним контактным проводом, устанавливают всего лишь не­сколько струн. Поэтому с целью повышения точности расчетов нагруз­ки, передающиеся с контактного провода на несущий трос, целесооб­разно рассматривать не как равномерно распределенные по всему про­лету, а как сосредоточенные в местах установки струн цепной подвес­ки (ряс. 86). Найдем эти нагрузки по схемам расположения струн в пролете, показанным на рис. 86.

Для схемы рис. 86, а имеем

Подставляя в это выражение значение g’_к из формулы (33), найдем

-126-

Уравнение провисания несущего троса цепной подвески при сосре­доточенных вертикальных нагрузках. Для вывода уравнения прови­сания несущего троса цепной подвески при передающихся с контакт­ного провода в местах установки струн сосредоточенных вертикальных нагрузках R воспользуемся схемами, показанными на рис. 87. Несу­щий трос будем рассматривать как свободно подвешенный провод, на­груженный равномерно распределенной нагрузкой от собственного веса g_тx и сосредоточенными силами R ₁ и R_ск.

Поскольку для схемы рис. 87, а нагрузка от веса контактного провода и гололеда на нем в пролете / полностью передается на несу­щий трос, то опорные реакции для схемы рис. 87, 6

-127-

Составив аналогичные уравнения изгибающих моментов для дру­гих точек несущего троса, в которых установлены струны (например, х = е + 2с и т.д.), можно найти его провесы в этих точках.

Уравнение провисания несущего троса цепной подвески при сосре­доточенных вертикальных и гори­зонтальных нагрузках. На несущий трос рессорных цепных подвесок, кроме нагрузки от собственного ве­са и нагрузок, передающихся с кон­тактного провода через струны, дей­ствуют еще сосредоточенные на­грузки Яр, обусловленные натяже­нием проводов рессорных струн. Эти нагрузки приложены к несуще­му тросу на расстоянии а от опор и направлены вниз под небольшим углом к горизонтали (рис. 88, а). Нагрузки от натяжения проводов рессорных струн можно заменить горизонтальными нагрузками Н_р и вертикальными Q, действующими в плоскости цепной подвески (рис. 88, б). Таким образом, в рес-

-128-

Сорных цепных подвесках несущий тpoc, кроме вертикальных, воспринимает также горизонтальные нагрузки, направленные вдоль несущего троса. В результате этого он имеет неодинаковое натяжение по длине пролета: в средней части (На длине / — 2 а) — натяжение Т, у опор (на длине а с каждой стороны от опоры) — натяжение Т-Н_Р. Натяжение проводов рессорных струн Н’р, которое ввиду малости углов наклона проводов к горизонтали можно считать равным Н_р, достигает 1,5—4,0 кН, что составляет от 10 до 30 % натяжения несу­щего троса Т.

Натяжения проводов рессорных струн, составляющие большую долю натяжения несущего троса, оказывают существенное влияние на форму кривой его провисания в пролете.

Для несущего троса рессорной цепной подвески, когда на него, кроме вертикальных, действуют также горизонтальные нагрузки, ос­тается справедливым выражение у_х = M_х /T_х.

Схема загруження простой балки для этого случая.показана на рис. 88, в. Изгибающие моменты от горизонтальных сил Н_p1 и Н_p2 соответственно: М₁ = Н_р1 у_а1; М₂ = Н_р2 у_а2.

Опорные реакции будут складываться из реакций от вертикальных сил V’ и реакции от горизонтальных сил V’’, т.е.

-129-

Аналогично нетрудно составить уравнений балочных изгибающих моментов и для других точек (например, x=e+ 2с и т. д.) несущего троса, в которых установлены струны, а затем найти провесы троса в этихточках.

Значения входящих в формулы (48) — (60) величин Q и Q' в большей степени, зависят от того, подвешен ли основной стержень сочленён­ного фиксатора к несущему тросу или к проводу рессорных струн. В последнем случае нагрузки Q и Q' оказывают большое влияние на форму кривой провисания несущого троса, и потому их не обходимо учитывать в расчетах.

С помощью приведених формул можно довільно точно определить провесы несущого троса цепной подвески в любой точке пролета

-130-

-131-

вые вдоль несущего троса и вызывающие изменения его натяжения от продета к пролету по мере удаления от компенсатора. Причиной из­менения натяжения может служить и сак компенсатор (заедание бло­ков и др.).

Чтобы представить влияние гололедной нагрузки на изменение высоты расположения контактного провода компенсированной подвес­ки, рассмотрим самую простую ее схему (см. рис. 85, а). Начнем со случая, когда контактный провод до появления гололеда располагает­ся в пролете беспровесно, т, е. f = 0. Тогда стрелу провеса несущего тpoca можно найти по формуле (44), т. е.

Таким образом, начальный провес контактного провода не влияет на изменение стрелы провеса несущего троса компенсированной под­вески при появлении на ее проводах гололеда.

По формуле (64) можно достаточно точно найти и изменение высоты расположения контактного провода от гололеда на проводах, сложных по схеме загрузки несущего троса (например, см. рис. 87 или 88) ком­пенсированных подвесок.

-132-

-133-

-134-

-135-

-136-

Дата добавления: 2015-09-03