Распределение Пуассона и его характеристики

Распределение Пуассона (Симеон Дени Пуассон (1781 – 1840) – французский математик)

Пусть производится п независимых испытаний, в которых появление события А имеет вероятность р. Если число испытаний п достаточно велико, а вероятность появления события А в каждом испытании мало (p£0,1), то для нахождения вероятности появления события А k раз находится следующим образом.

Сделаем важное допущение – произведение пр сохраняет постоянное значение:

Практически это допущение означает, что среднее число появления события в различных сериях испытаний (при разном п) остается неизменным.

По формуле Бернулли получаем:

При том что n велико вместо Pn(k) найдем limPn(k)(при n сртем к бесконечн) и найдем приближенное значение отыскиваемой величины

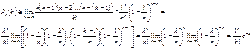
Получаем формулу распределения Пуассона:

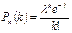
Дата добавления: 2015-08-21