
|
Читайте также: |
2.4.1. Хлопчик кинув з поверхні Землі м’яч під кутом 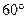 до горизонту з початковою швидкістю
до горизонту з початковою швидкістю 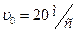 . Через
. Через 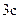 м’яч впав на горизонтальний дах будинку. Визначити висоту будинку та відстань, яку пролетів м’яч по горизонталі, вважати, що
м’яч впав на горизонтальний дах будинку. Визначити висоту будинку та відстань, яку пролетів м’яч по горизонталі, вважати, що 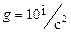 .
.
Дано:
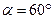
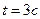

|
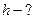
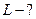
|
Аналіз
 Оберемо систему відліку, тілом відліку якої є Земля. Початок системи координат знаходиться в точці
Оберемо систему відліку, тілом відліку якої є Земля. Початок системи координат знаходиться в точці 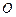 , з якої здійснимо кидок. За початок відліку часу візьмемо момент часу, коли тіло кинуто. Оскільки на тіло діє лише сила тяжіння (опором повітря нехтуємо), то координата
, з якої здійснимо кидок. За початок відліку часу візьмемо момент часу, коли тіло кинуто. Оскільки на тіло діє лише сила тяжіння (опором повітря нехтуємо), то координата 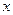 тіла з часом змінюється так само, як і для прямолінійного рівномірного руху:
тіла з часом змінюється так само, як і для прямолінійного рівномірного руху: 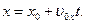
Оскільки 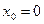 і
і 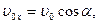 то
то 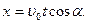
Координата 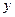 змінюється так само, як і для прямолінійного рівноприскореного руху:
змінюється так само, як і для прямолінійного рівноприскореного руху:
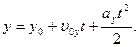
Оскільки, 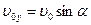 ,
, 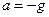 , то
, то 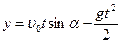 .
.
Отже, 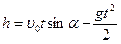 , a
, a 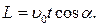
Обчислення:
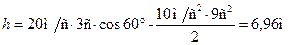 ,
, 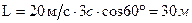
Відповідь: висоту будинку рівна 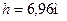 , а відстань, яку пролетів м’яч по горизонталі –
, а відстань, яку пролетів м’яч по горизонталі – 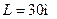 .
.
2.4.2. Відстань між двома населеними пунктами автомобіль проїхав із середньою швидкістю 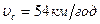 за час
за час 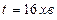 . Розгін і гальмування тривали
. Розгін і гальмування тривали 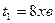 , а решту шляху автомобіль рухався рівномірно. Яку швидкість
, а решту шляху автомобіль рухався рівномірно. Яку швидкість 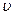 мав автомобіль під час рівномірного руху.
мав автомобіль під час рівномірного руху.
Дано:
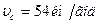
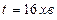
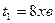
| СІ
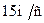
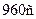
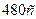
|
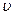 –? –?
|
Аналіз
 Зобразимо графік залежності швидкості автомобіля від часу. Ділянка
Зобразимо графік залежності швидкості автомобіля від часу. Ділянка 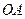 відповідає розгону автомобіля, ділянка
відповідає розгону автомобіля, ділянка 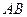 – рівномірному руху, ділянка
– рівномірному руху, ділянка 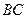 – його гальмуванню. Шлях, що пройшов автомобіль чисельно рівний площі трапеції, яка утворена графіком швидкості:
– його гальмуванню. Шлях, що пройшов автомобіль чисельно рівний площі трапеції, яка утворена графіком швидкості: 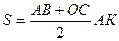 або
або 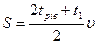 .
.
З іншого боку, із означення середньої швидкості: 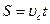 . Отже,
. Отже,
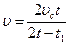 .
.
Обчислення:
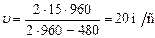 .
.
Відповідь: швидкість, яку мав автомобіль під час рівномірного руху рівна 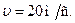
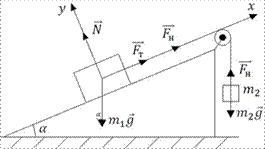
2.4.3. До вантажу масою 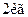 , що знаходиться на похилій площині з кутом нахилу
, що знаходиться на похилій площині з кутом нахилу 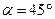 прив’язана нитка, яка перекинута через блок. Визначте за яких значень маси
прив’язана нитка, яка перекинута через блок. Визначте за яких значень маси 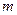 вантажу, що підвішений до другого кінця нитки система перебуватиме в рівновазі. Коефіцієнт тертя по похилій нитці. Коефіцієнт тертя по похилій площині дорівнює
вантажу, що підвішений до другого кінця нитки система перебуватиме в рівновазі. Коефіцієнт тертя по похилій нитці. Коефіцієнт тертя по похилій площині дорівнює 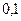 ?
?
Дано:
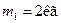
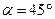
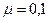
|
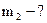
|
Аналіз
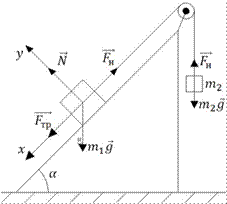 Система може перебувати в русі у двох напрямах:
Система може перебувати в русі у двох напрямах:
1) вантаж масою 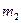 рухається вниз, а вантаж масою
рухається вниз, а вантаж масою 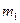 вгору по похилій площині;
вгору по похилій площині;
2) вантаж масою 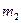 рухається вверх, а вантаж масою
рухається вверх, а вантаж масою 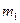 вниз по похилій площині.
вниз по похилій площині.
Розглянемо перший випадок. Визначимо максимальне значення маси 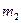 , за якої система перебуватиме у рівновазі. За цієї умови сила тертя направлена вниз по похилій площині.
, за якої система перебуватиме у рівновазі. За цієї умови сила тертя направлена вниз по похилій площині.
Запишемо другий закон Ньютона для кожного з тіл зображених на рисунку.
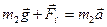 ;
; 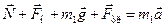
Оскільки, розглядає граничний випадок (початок руху), то вважатимемо 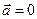 Тоді в проекціях на вісі
Тоді в проекціях на вісі 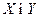 , маємо:
, маємо:
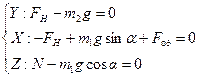
Враховуючи, що 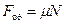 , a
, a 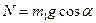 , то
, то 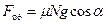 .
.
 Розв’язуючи перші два рівняння, маємо:
Розв’язуючи перші два рівняння, маємо: 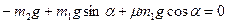 звідки
звідки 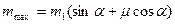 .
.
Розглянемо другий випадок. Визначимо мінімальне значення маси 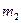 , за якої система перебуватиме в рівновазі. Сила тертя між вантажем масою
, за якої система перебуватиме в рівновазі. Сила тертя між вантажем масою 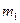 і похилою площиною буде направлена вгору по похилій площині.
і похилою площиною буде направлена вгору по похилій площині.
Запишемо другий закон Ньютона для кожного з тіл: 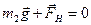 ;
; 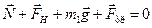
У проекціях на вісі 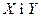 , маємо:
, маємо: 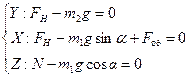
Оскільки, 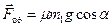 , а
, а 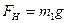 , то
, то 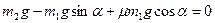 , звідси
, звідси
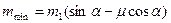 .
.
Отже, система тіл перебуватиме в рівновазі за умови:
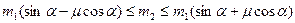 .
.
Обчислення:
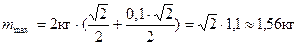
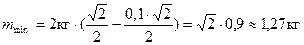
Відповідь: за таких значень маси 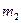 вантажу, що підвішений до другого кінця нитки система перебуватиме в рівновазі:
вантажу, що підвішений до другого кінця нитки система перебуватиме в рівновазі: 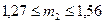 .
.
2.4.4. Кулька масою 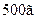 , підвішена на нитці завдовжки
, підвішена на нитці завдовжки 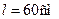 , рухається по колу в горизонтальній площині рівномірно. Визначити кутову швидкість обертання кульки і силу натягу нитки, якщо нитка утворює з вертикаллю кут
, рухається по колу в горизонтальній площині рівномірно. Визначити кутову швидкість обертання кульки і силу натягу нитки, якщо нитка утворює з вертикаллю кут 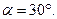
Дано:
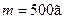
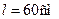 
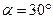
| СІ
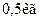
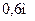
|
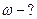
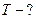
|
Аналіз
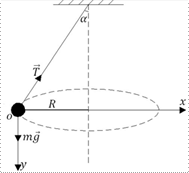 Вважаючи нитку невагомою і нерозтяжною, запишемо другий закон Ньютона у векторній формі:
Вважаючи нитку невагомою і нерозтяжною, запишемо другий закон Ньютона у векторній формі: 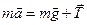
У проекціях на вісі 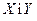 , маємо:
, маємо:
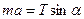 (1)
(1)
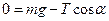 (2)
(2)
де 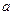 – доцентрове прискорення.
– доцентрове прискорення.
З другого рівняння: 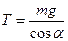 .
.
З першого рівняння: 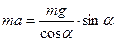 =>
=> 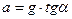 . Оскільки
. Оскільки 
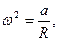
де 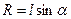 , маємо
, маємо 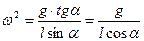 =>
=> 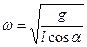 .
.
Обчислення:
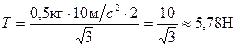 .
.
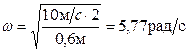 .
.
Відповідь: кутову швидкість обертання кульки рівна 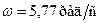 , а сила натягу нитки –
, а сила натягу нитки – 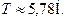
 2.4.5. На балку, що лежить на двох опорах
2.4.5. На балку, що лежить на двох опорах 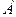 і
і 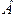 , треба покласти вантаж масою
, треба покласти вантаж масою 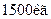 . Довжина балки
. Довжина балки 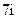 . На якій відстані від опори
. На якій відстані від опори 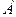 треба розмістити вантаж, щоб він тиснув на неї із силою
треба розмістити вантаж, щоб він тиснув на неї із силою 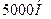 ? Вважаючи масу балки не враховувати.
? Вважаючи масу балки не враховувати.
Дано:
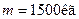
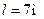
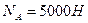
|
|
Аналіз
Нехай вісь обертання балки проходить через точку 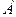 . Звичайно, можна обрати іншу точку, наприклад
. Звичайно, можна обрати іншу точку, наприклад 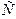 або
або 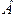 . з умови рівноваги балки випливає рівність для сил:
. з умови рівноваги балки випливає рівність для сил: 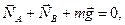
звідси 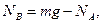 або
або 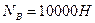 .
.
З умови рівноваги балки маємо рівність для моментів сил відносно точки 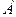 :
: 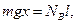 звідси
звідси 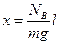 .
.
Обчислення:
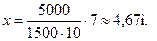
Відповідь: на відстані 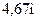 від опори
від опори 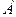 треба розмістити вантаж, щоб він тиснув на неї із силою
треба розмістити вантаж, щоб він тиснув на неї із силою 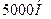 .
.
2.4.6. Під яким мінімальним кутом до горизонту можна приставити до гладенької вертикальної стіни однорідну драбину, щоб вона не впала? Коефіцієнт тертя між драбиною і горизонтальною підлогою 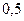 .
.
Дано:
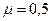
|
 –? –?
|
 Аналіз
Аналіз
На малюнку показані сили, що діють на драбину. Запишемо умову рівноваги драбини в разі відсутності поступального руху: 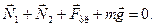
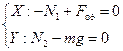 . Якщо довжина драбини
. Якщо довжина драбини 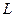 , то умова рівноваги драбини в разі відсутності обертального руху відносно осі, що проходить через точку
, то умова рівноваги драбини в разі відсутності обертального руху відносно осі, що проходить через точку 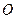 має вигляд:
має вигляд:
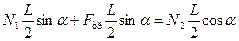 =>
=> 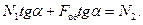
Для визначення кута 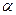 нам достатньо таких рівнянь:
нам достатньо таких рівнянь:
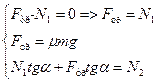 =>
=> 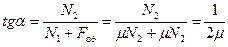
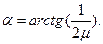
Обчислення:
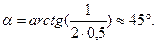
Відповідь: під кутом 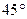 до горизонту можна приставити до гладенької вертикальної стіни однорідну драбину, щоб вона не впала.
до горизонту можна приставити до гладенької вертикальної стіни однорідну драбину, щоб вона не впала.
2.4.7. У нерухомому човні на відстані 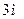 один від одного сидять
один від одного сидять 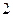 рибалки. Маса човна
рибалки. Маса човна 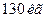 , маса першого рибалки
, маса першого рибалки 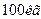 , другого –
, другого – 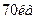 . На яку відстань зміститься човен, якщо рибалки поміняються місцями?
. На яку відстань зміститься човен, якщо рибалки поміняються місцями?
Дано:
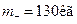
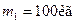
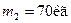
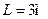
|
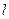 –? –?
|
Аналіз
Нехай рибалки у човні переміщуються по черзі. Записуємо закон збереження імпульсу для переміщення рибалки масою 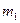 :
: 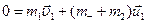 , (1)
, (1)
де 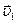 – швидкість рибалки масою
– швидкість рибалки масою 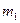 відносно дна (або берега),
відносно дна (або берега), 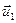 – швидкість човна з другим рибалкою відносно берега. Нехай рибалка масою
– швидкість човна з другим рибалкою відносно берега. Нехай рибалка масою 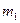 пересувається відносно човна зі швидкістю
пересувається відносно човна зі швидкістю 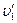 . Тоді відповідно до закону додавання швидкостей
. Тоді відповідно до закону додавання швидкостей 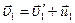 . (2)
. (2)
Підставляючи (2) в (1), маємо: 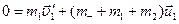 .
.
У проекції на вісь 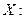
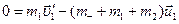 .
.
Враховуючи, що 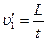 ,
, 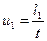 , де
, де 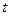 – час переміщення рибалки по човну, дістанемо:
– час переміщення рибалки по човну, дістанемо: 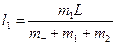 .
.
Аналогічно, для рибалки масою 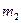 , що рухається, знайдемо
, що рухається, знайдемо
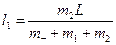
Тому: 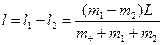 .
.
Обчислення:
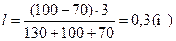
За умови, що 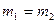 загальне переміщення човна
загальне переміщення човна 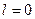 .
.
2.4.8. Визначити амплітуду, частоту і період гармонічних коливань матеріальної точки, якщо її максимальна швидкість під час коливань дорівнює 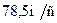 , а максимальне прискорення –
, а максимальне прискорення – 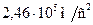 . Вважаючи початкову фазу нульовою, а коливання такими, що відбуваються за законом косинуса, записати рівняння коливань і побудувати його графік.
. Вважаючи початкову фазу нульовою, а коливання такими, що відбуваються за законом косинуса, записати рівняння коливань і побудувати його графік.
Дано:
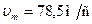
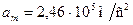
|
 –? –?
 –? –?
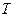 –? –?
|
Аналіз
Максимальна швидкість 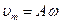 , (1)
, (1)
а максимальне прискорення 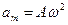 (2)
(2)
де 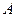 – амплітуда;
– амплітуда; 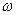 – циклічна частота коливань. Розділивши рівняння (2) на рівняння (1), одержимо
– циклічна частота коливань. Розділивши рівняння (2) на рівняння (1), одержимо
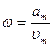 .
.
Частота коливань 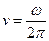 .
.
Амплітуду коливань знаходимо з рівняння (1): 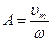 .
.
Обчислення:
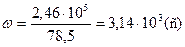 .
.
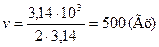 .
.
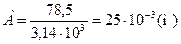
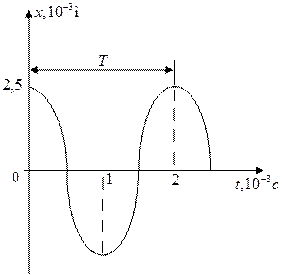 Підставляючи у рівняння коливань
Підставляючи у рівняння коливань 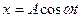 числові значення амплітуди і циклічної частоти, дістаємо
числові значення амплітуди і циклічної частоти, дістаємо 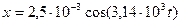
Графік коливання, виражений формулою (3) показано на рисунку.
Дата добавления: 2015-08-21; просмотров: 600 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Механічні коливання і хвилі. Елементи акустики | | | Добірка фізичних задач з механіки 1 страница |